皮带式固态不规则块状矿物连续称重机设计【全套含CAD图纸、说明书】
收藏
资源目录

压缩包内文档预览:
编号:17376242
类型:共享资源
大小:4.11MB
格式:ZIP
上传时间:2019-04-06
上传人:机****料
认证信息
个人认证
高**(实名认证)
河南
IP属地:河南
50
积分
- 关 键 词:
-
全套含CAD图纸、说明书
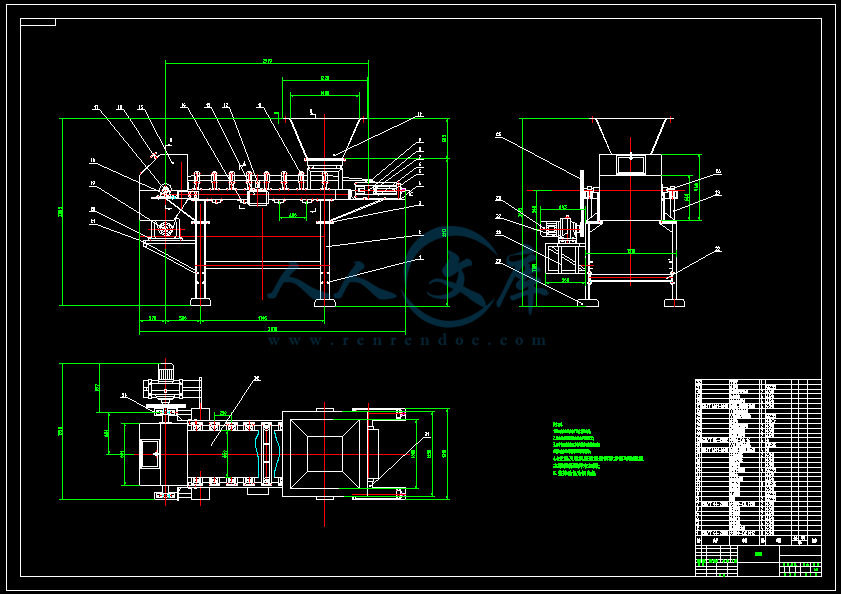
皮带式固态不规则块状矿物连续称重机设计
皮带式固态不规则块状矿物连续称重机设计说明书
- 资源描述:
-











- 内容简介:
-
编号: 毕业设计(论文)外文翻译(译文)院 (系): 机电工程学院 专 业: 机械设计制造及其自动化 学生姓名:学 号: 指导教师单位: 姓 名:职 称: 摆式磨床中连杆颈的原位测量与校正摘 要在大规模生产的车用发动机曲轴中,使用振动研磨机的追针磨是一种被广泛接受的方法来实现灵活,高效的性能。然而,连杆颈的偏心运动使得很难为轮廓精度提高制定一个同进程的圆度测量方案。这里,一个新的拥有很高扫描速度的原位测量圆度策略被提出了。该测量机构是由一个V形块和一个自适应伸缩支架组成的。伸缩支架和V型块的摆动图案被用于相等的角度间隔信号取样分析。因此,圆度误差信号是通过使用V型块圆度测量方法的一个小信号模型和快速傅立叶变换在频域范围内提取的。为了落实振荡磨床数控坐标系中的圆度数据,变换函数需根据连杆颈磨削方法的运动模型导出。计算机模拟表明曲轴部件的旋转位置和V型块上位移探头的扫描角之间的关系,以及由旋转中心漂移引入的影响。标准调查表明理论分析的有效性和新策略的可行性。关键词:曲轴;圆度测量;伸缩摆动支撑;磨床追针磨1. 介绍随着小排量和更高转速的发展趋势,曲轴连杆轴颈的圆度精度正影响着车辆发动机的工作效率,稳定性和寿命。为了提高加工精度和效率,基于振荡研磨机的连杆颈磨削方法已被开发并在曲轴的制造中广泛应用。这种方法在大批量生产中灵活性很高。另一方面,由于磨轮的磨损、伺服系统响应误差、塑性变形等,振动研磨机仍然面临连杆轴颈的轮廓精度控制的问题。为了最大限度地减少弹性变形的影响,沃尔什对磨削力模型进行了研究并应用于兰迪斯CP曲轴磨床。此外,港华等人已经在曲轴磨床中研究了基于神经网络的路径补偿方案。然而,由于其独特的造型,曲轴组件的刚度比其他普通轴刚度差。曲轴组件弹性变形的程度是受内应力,夹紧应力,磨削力等方面的不同而影响。此外,因为轴承的轮廓误差引起的重复震动,使得在振荡研磨机中固定中心架的安装还导致夹紧曲轴组件显著的姿态变化。因此,销轴颈的圆度误差不能仅通过改进研磨过程的轨迹精度来消除。在曲轴制造应用中原位测量成为连杆轴颈的圆度校正具有竞争力的解决方案。目前,有几种方法已经被开发并用于机械圆度的检查,例如辐线法、多探针法、V型块方法。但是,在振荡研磨机中销轴颈的原位圆度测量法所面临的挑战可以用图1来说明。扩大的红色部分显示的是加工中的连杆轴颈,它在整个制造过程中遵循着一个偏心运动。几何中心的这种显著变化对传统圆度的检查方式来说是不可接受的,即便是使用V型块方法。原位测量机构外形的可用空间也受到砂轮、曲轴组件本身、以及冷却液的喷嘴的限制,更不用说由火花磨削和冷却液雾所引起的恶劣环境了。在某些商业应用中,拥有专利权支撑的V形块方法已被报道应用于在曲轴磨床原位的圆度测量。然而,精密测量机构已经显示出诸多弊端,如调整难度大、成本高、扫描速度慢等。在这一研究中,基于V型块法的新原位圆度测量方案重点针对的是扫描速度和稳定性。采用自适应伸缩支撑机构的测量机构结构简单,尺寸紧凑。为了保证信号的完整性,被纯净的压缩空气密封的接触位移探头被用于圆度信号获取。伸缩支架和V型块的摆动角度的原理用于以均等角度间隔信号采样算法的发展分析。因此圆度误差是使用V形块圆度测定方法和快速傅立叶变换的一个小信号模型在频域范围中提取的。对于原位圆度校正的目的,转换函数也可从振动研磨机的数控系统中导出来。2. 原位圆度测量装置 当使用V型块方法进行原位检查时,因为目标连杆轴颈被牢固地夹紧,原位的圆度的测量机构应包括以下功能:a) 在磨削和扫描过程中捕获曲轴组件的所有旋转位置的目标连杆轴颈。b) 在目标连杆颈正截面提供至少两个自由的维度,以避免V形块和曲轴组件之间的刚性碰撞。c) 保持探针稳定的扫描姿势或具有固定且已知的原理的变化的姿态。然后原位测量机构可以调整由目标连杆颈的非圆轮廓和偏心运动所造成的V形块不规则的运动。因此,V形块和目标连杆颈之间的柔性接触可以随着稳定的扫描过程而实现。2.1 自适应伸缩支撑件考虑上述三个原则,基于自适应伸缩支撑件提出了一个原位圆度测定机构,它的几何原理如图2所示。接触位移探针被放置在V形块的轴线位置,它的方向指向目标连杆颈中心。目标连杆轴颈绕曲轴旋转中心Ow以Re为偏心距作偏心运动。自适应伸缩支撑机构具有直线导轨和内部弹性力可以撑起V形块和位移探头的组合。支持的终端点A铰接在机身上,另一个末端与V形块连接。在扫描期间,伸缩支撑机构开始自适应地展开,随着曲轴部件的旋转而膨胀或收缩。因此,目标连杆颈的偏心运动被中和掉了。实际上,自适应伸缩支撑件可以使用标准的气动元件,如直线轴承气缸、气动幻灯片等。在压缩空气的激励下,V形块能够保持与连杆颈表面的紧密和柔性接触。为了保证曲轴组件的所有旋转位置能够可靠地接触,自适应伸缩支撑件的最小行程应大于2倍的偏心距。在摆动运动中关节点A的旋转的自由度也是必不可少的。 由于受到支撑机构摆动角的干扰,当曲轴组件以恒定的速度旋转时,位移探针的扫描角并不是绕连杆颈中心Op线性增加的,而是遵循一个固定的原则即受到原位测量机构和曲轴部件几何参数约束的一个原则。在图2中所建立的坐标系Owxy是用来分析摆动角度的变化原理和扫描角的非线性特性。在坐标系中,X轴指向线段OwA ,A点的位置在扫描过程中保持不变。连杆颈被假定为半径为Rp和偏心距为Re的一个标准圆柱体。因此,摆动角,扫描角度和曲轴组件的旋转角满足以下关系:其中,XA为A点的横坐标,作为输入,可以通过两个公式的组合精确地计算出来,推导函数表示为使用JL4G15曲轴产品的参数(Rp 为22 mm, Re 为39.4 mm ),根据对振荡研磨机实际调查OwA的长度被设定为364毫米,通过求解公式(2)获得的曲线。如图3所示,和之间的关系是非线性的,这意味着位移探头的扫描角的增长速度与曲轴组件的稳定旋转速度间的关系不是恒定的。然而,是单调增加的,并服从一个固定的变分原理,这一原理仅由等式(2)确定。这两个特征在扫描过程中的是很重要的。此外,为了显示曲轴部件的旋转中心漂移的效果,一个振幅为0.01mm的随机函数被引入到Ow.点。然后为了确认扫描角的扰动而进行计算机的模拟。图4呈现的是的偏差曲线,在这一偏差曲线中峰峰值为11.0772角秒。由这样的干扰而引起的探测信号的相位抖动可以通过下面式子来估算其中err代表瞬时偏差值,NSS是沿着连杆颈表面一圈圆周上的采样点。在大规模生产中,连杆颈圆度检查的最大谐波次数通常被设置为50次,因此,实际上128的数值对于NSS来说是足够的,所以Phe的峰峰值计算为1.094。考虑到在径向方向上接触式位移探头的有限分辨率这个相位抖动弱到足以被忽略。根据前面的分析,由V形块和自适应伸缩支撑件构成的原位测量机构具有结构简单,体积小,和对曲轴部件的旋转中心漂移的敏感度小等优点。在振荡研磨机的极端环境中这些特征对可靠和高速扫描操作来说是不可缺少的前提。2.2 等角度间隔的采样算法 通常,目标连杆颈中心Op周围的探测信号的相等角度间隔采样对圆度分析程序来说是必要的。然而,自然的信号采集过程通常需要时间作为采样参考更不用说直接测量扫描角度的难度有多大了。这里,针对已取得的以时间为基础的探测数据的后置处理来说,一个两步相等角度间隔的采样算法得到了实现。图5所示的是信号流程图。在图5中D(t)表示位移探头的实时信号;(t)的表示转盘内的旋转编码器的实时信号,它用来驱动曲轴部件的旋转。同步相等的时间间隔采样阶段将D(t)和(t)转换为两个离散的数据阵列,它们分别被描述为DT(n)和T(N)。此过程是相等的角度间隔采样算法的第一步骤。为了计算相等角度间隔采样数据阵列d (n)即一个常规的扫描角度阵列,(n)用下面的等式定义并初始化然后用公式(2),将(n)转换换成(n),作为第二阶段的再采样参考。关于在一次循环中沿着连杆轴颈的圆周上的128个采样点和用Visual Basic6.0开发的数值算法的例子见附录A.。(n)为重采样参考,d (n)在第二步骤中获得,则一个线性插值模块可以表示为其中,n的范围是1到Nss。为了抑制线性插值的算法错误,第一阶段的采样密度应高于第二阶段。在这项研究中,时域中的采样率是5000赫兹,转盘的旋转速度.设定为20 r/min。从而沿连杆颈圆周表面的采样点为每转15000个,而对于圆度分析的采样点都是每转128个。这意味着,在第一阶段的取样密度是第二阶段100倍以上。 随着等角度间隔采样算法的成熟发展,即使在扫描过程始终受到原位测量机构的周期性摆动运动的干扰,以目标连杆颈均匀角度基准获取探测信号是行得通的。3 V型块圆度测量方法V形块圆度测量方法的原理如图6所示,其中表示V形块的夹角。将位移探头安装在V型块的中心线上,物块的圆度状态可以通过在旋转扫描过程中获取的探针信号进行检测。因为物块在V形块和自身表面间的切点A和B间滚动,而非物块的中心,所以在扫描操作过程中并不需要一个稳定的和精确的旋转中心。如果点A和点B始终满足一个标准弧的条件,那么探测信号的交流分量将代表圆度误差,而直流分量与物块的半径R的偏差有关。然而,对真正的机械组件来说,圆度误差不断地分布在整个圆周上,这无疑会导致A和B两点间的表面变形。不可避免地,瞬时旋转中心会从理想位置转移,从而探测信号在扫描期间将会受到干扰。因此,根据图6所示,位移探头的瞬间值可用如下函数式表示:其中A,B和C分别代表A,B和C点的轮廓偏差。该公式表明该位移探测器的信号值是轮廓偏差同时在扫描点和两个切点的耦合的结果。3.1 小信号模型为了绘制出探查信号和连杆颈精确的圆度误差之间的关系,建立一个用于V形块圆度测定方法的小信号模型。如图7所示的几何原理,因为目标连杆颈是用于扫描操作的有源元件,它的垂直中心线作为Y轴。垂直中心线和理想圆形轮廓之间的交点作为原点,就这样建立起了一个坐标系OSxy。 目标连杆轴颈轮廓可用圆度误差函数r()和半径参数Rp,来定义,其中表示沿中心点OP的角位置。在初始状态下,如果C点对准目标连杆颈零角度的位置,那么A,B,C点的轮廓偏差的函数可以推导为在初始状态下,考虑到在点A和B的表面的变形, V形块顶点D的瞬时坐标值可由如下式子导出在上面的等式中,yd是顶点D理想的坐标值,线段DOp和DOp间的长度差代表施加在探针信号上的耦合元件,其可表述为 在精密磨削阶段,r()的幅度通常比Rp少得多,所以,不等式 的推测是合理的。因此,通过结合方程(7) - (9),eab(t0)可以简化为 用一标准的圆柱体(半径= Rp)对探针调零,并规定收缩方向作为正方向,位移探头的初始状态信号值d(t0)可以表示为 根据上述等式,d(t0)等于a(0), b(0)和 c(0)的线性加权求和。显然,这种线性加权求和的原则适用于目标连杆颈所有的角度位置。因此,V形块圆度测量方法的小信号模型被进一步合成为其中,在等式(12)中,d()表示由目标连杆颈的角位置中声明的探测信号。权重系数的值k仅取决于V形块的夹角。同时还发现,该小信号模型不能直接用于圆度误差的求解,因为圆度求解是方程(12)的逆过程。并且式(12)中的四个部分之间的关系不能由任何单一采样点来确定。然而,对于一个纯粹的正弦或余弦信号来说,探测信号和圆度误差信号之间的关系可以简化为一个振幅增益和相移值。这意味着可以从等角度间隔采样算法中用一组整体的采样数据阵列d(n)在频域中进行圆度误差分析。因此,小信号模型被进一步转化为频域中的一个映射表。例如,以71作为一个夹角,使用统一的正弦信号作为目标连杆轴颈的圆度误差,各谐波分量的振幅增益和相移值适合于使用Visual Basic 6.0开发了一种数字算法的探针信号。更多详细内容附于附录B。表1是小信号模型的映射表。在计算过程中,零振幅增益是在第32次谐波分量和第34次谐波分量中观察到的。类似的现象在文献11中也有记录。这种谐波抑制的效果可以通过调整夹角得到部分补偿。在这项研究中,将谐波抑制频带移位到高频区更为有效,这在工程应用中比低频区域更有价值。3.2 圆度误差的提取如图8所示的是圆度误差提取的算法结构。图中REV2REVm代表各谐波成分的在映射表中的逆算子,包括振幅增益和相移值。为了利用该数据阵列d (n),引入快速傅立叶变换(FFT)模块将包含在d (n)中所有谐波成分分离,其分别表示为d0, d2dm。然后直接分量d0乘以一个克尔系数便可修复连杆颈的半径偏差。根据图7,克尔系数可以表示为 由目标连杆轴颈圆度误差引起的的谐波分量d2dm由REV2REVm处理,于是可恢复圆度误差信号。所以,每个反向运算符输出的总和就是圆度误差信号r(),其可用下面的等式描述其中m是圆度分析程序的截止频率,ampn和n表示dn分量的振幅和相角。coen和n表示振幅增益和第n次谐波分量的相移值,如表一中所示。 值得一提的是,圆度测量和校正的频带可以通过对于不同原位的情况下选择所需的谐波成分进行灵活调整。用Visual Basic 6.0开发的圆度提取程序详见附录C。4. 连杆颈的圆度校正 在将圆度误差信号r()注入到磨削程序之前,用于原位圆度测量的坐标系必须与CNC坐标系统同步,这是用于连杆轴颈加工。此外,因为r()是建立在目标连杆颈角位置的基础上的,并且针追磨的运动模型在振荡研磨机中具有非线性特性,所以在圆度校正程序中使用r()也需要格式转换。4.1 同步坐标系 在大多数情况下,振荡研磨机的CNC坐标系是一个C-X轴联动模式。其中,C轴用来驱动曲轴部件的旋转,被当作主轴。X轴用来驱动砂轮实现进给运动和摆动运动,通常作为从动轴。因此,对于数控坐标系统的控制基准是C轴的旋转角,其在前面的分析中也被定义为曲轴部件的旋转角。另一方面,在原位圆度测量系统中,参考变量显然是目标连杆颈的角位置。从而,根据图2知如果线段OwA的长度可以确定,可以便可用的瞬时值来计算。如果在CNC坐标系中线段OwA的方向可以确定,则目标连杆颈的角位置和探测扫描角之间的零点差便可以得到验证。 然而,在实际情况下虚线段OwA不能直接被观察,很难用常规的方法来测量线段OwA,这导致难以建立原位测量机构的几何模型。因此,原位圆度测量系统的同步坐标以间接模式来实现。图9所示的是间接同步方法的理论。旋转编码器被暂时装在A点以检测支架的摆动角度。转动曲轴组件作整体旋转运动,使得最高摆点和最低摆点的中心线对准OwA方向。对应的瞬时值表示在CNC系统中的同步时刻。此外,线段OwA的长度可推导得其中p代表C轴分别对应于最大摆动角度和最小摆角的角度差。p是摆动角的峰峰值。因为在支架与OwA对准的时刻总是对应于目标连杆颈0或180的角度位置,因此在追针磨程序中A点的旋转编码器可能将永久地用于新的夹紧曲轴组件的初始阶段的检测。4.2 圆度数据实现 根据销的追磨削的运动模型从振幅和相位调整的变换函数推导出了r()。如图10所示,Ot是砂轮的中心,当连杆颈随曲轴组件绕Ow一起旋转时,砂轮和连杆颈通过车轮托架位置的同步调整保持相切。因此,该变换函数推导为其中,在方程 (17)中,为圆度校正信号的修复的相位和振幅系数在CNC坐标系中可用和定义,结合方程(15),(17)和(18),追磨削的圆度校正信号rcomp()可被合成为 5. 实际调研我们的实验室构建了原位圆度测量和校正系统的原型。原型被装在振荡研磨机上,以验证所提出的测量机构的工程性能和相应的信号处理算法。V形块的夹角被指定为71。具有0.1微米的分辨率,0.5微米(P-P)精度,12毫米全音频和42米每分钟的最大响应速度的索尼DK812VR磁力计被选作为接触式位移探头。该原型的控制单元是基于数字信号处理器(DSP)TMS320F2812硬件平台和CCS3.3交叉编译环境。小信号模型的信号处理算法、频域分析法和原位工艺控制的发展是基于Visual Basic6.0环境。数控系统和原型之间的实时数据链接使用工业以太网接口和TCP / IP协议。实际调查系统的概述如图11所示,其中CYTEC CRT/350转盘作为C轴。液体静压导轨和一个西门子1FN3900-4WC的线性电机结合形成X轴。砂轮由亨氏飞格MSP230马达主轴驱动, MARPOSS P7系统用于砂轮的线上平衡。伺服模块和摆动磨床的数控系统分别基于西门子SIMODRIVE611D和840D SINUMERIK。5.1 原位圆度测量为了验证所提出的测量方案的准确性,在JL4G15Y曲轴组件上做一个对比实验,将ADCOLE1100离线检测中心作为标准测试仪器。原型的截止频率和标准测试仪器都设置到50。表2显示了实验研磨的工艺参数。追针磨过程的一个标准数控程序无额外数据补偿地应用于样品组件上。图12示出从样机获得的第一根连杆轴颈的圆度误差波形,图中峰峰值为7.871微米。有着相同的成分,图13显示用ADCOLE1100获得的圆度误差数据,其峰峰值为7.990微米。使用离线数据(图13中)作为参考,图14给出了在原位测量数据的偏差曲线,最大独立偏差值是0.47微米,整周的均方根偏差值是0.171微米。这些亚微米级的偏差表明原位的圆度校正在微米范围内的可能性。5.2 原位圆度校正 首先,将样品成分用标准销追磨削程序进行处理,接着进行原位圆度测量。用所获得的圆度校正信号(等式(19)所示)生成原位圆度校正数据并植入到数控程序中。然后,将二次研磨步骤应用到每个连杆颈。二次研磨后的第一根连杆轴颈的残余圆度误差将由原位原型测量出,并在图15中给出。圆度误差的峰峰值为2.689毫米,最大独立的圆度误差为1.505毫米。即使振荡研磨机和原型都受到具有显著不确定性和时间变化的几个因素的干扰,目标连杆颈的圆度误差也被有效地通过在线测量和即时校正的优势而抑制。为了进行比较,还进行另一个实验,这个实验具有相同的研磨过程但没有圆度校正数据。获得相应的圆度误差并在图16中给出的,峰峰值为7.298毫米。没有原位测量和校正只能轻微地降低圆度误差。这可以通过标准研磨程序和二次磨削程序之后进行的一个普通精磨阶段来说明。这个精细研磨阶段是由对于C轴的旋转速度为0.005mm/s的6秒时长和0mm/s的9秒时长构成,在这一阶段,尽量减少进给参数在最终产品的原位测量精度和轮廓精度上的影响。6. 结论显示已表明,在振荡研磨机中使用的V形块法对连杆颈进行原位圆度测量和校正是可行的和有效的。通过紧扣连杆颈偏心旋转的性质,所设计的测量机构(示于图2)提供了许多优势,如结构简单、体积小、和扫描速度高。基于测量机构的几何原理和V形块圆度测量方法的小信号模型而新开发的信号处理算法(在附录A-C给出)不仅可以实现连杆颈轮廓误差的等角度间隔采样,也可以分离的圆度误差信号,并为圆度的校正产生补偿数据。通过使用离线曲轴检查仪ADCOLE1100的对比实验,研究在振荡研磨机中原型系统的性能,测量的精准程度对圆度校正来说是足够的。在一次圆度校正尝试中,连杆颈的峰值圆度误差由7.871毫米减至2.689毫米,独立圆度误差抑制在1.505毫米。这意味着,连杆轴颈在微米范围内的圆度精度可以直接在夹紧状态下进行检查。这种计量给整个生产过程中带来了附加值,例如缩短加工时间,降低废品率等。然而,应该指出的是,现在所提出的策略也有不足。第一个问题是,V型块和位移探头的热膨胀和收缩长期影响半径的测量精度,当前的解决方案是增加校准时间。另一问题是,该接触位移探头并不能区分连杆颈表面和冷却液体膜的表面。一些油性冷却液可能导致一定程度的系统偏差。所有这些因素可能会增加测量的不确定性并限制了应用领域,因此这些误差来源的调查必须得谨慎进行,结果将在不久的将来发布。致谢笔者想感谢中国国家自然科学基金会。这份报告的工作也得到中国国家高技术研究发展计划863的支持。窗体顶端窗体底端参考文献1 M.K.P. Alex, A. Taylor, Science review of internal combustion engines, Energy Policy (2008) 46574667. 2 Dong Yan, Vehicle turbocharged small-displacement gasoline engineeffective solution to CO2 emission reduction of traditional gasoline power-train, Auto Eng. (2010) 4549. 3 H.K. Tonshoff, B. Karpuschewski, T. Mandrysch, I. Inasaki, Grinding process achievements and the consequences on machine tools challenges and opportunities, CIRP Ann. Manuf. Technol. (1998) 651668. 4 Duan Shaolin, Mao Zeyong, Song Liqiang, Current status and development trend of crankshaft machining techniques and equipments, Int. Combust. Engines (2010) 2730. 5 H.-C. Mohring, O. Gummer, R. Fischer, Active error compensation in contour-controlled grind
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号