皮革剪板机设计
36页 14000字数+说明书+任务书+外文翻译+6张CAD图纸【详情如下】
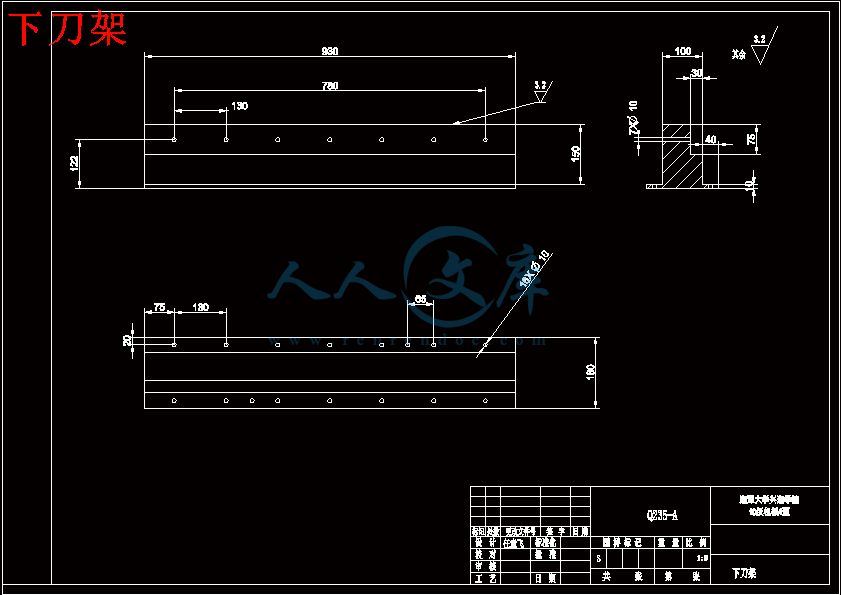
下刀架.dft
下刀架.dwg
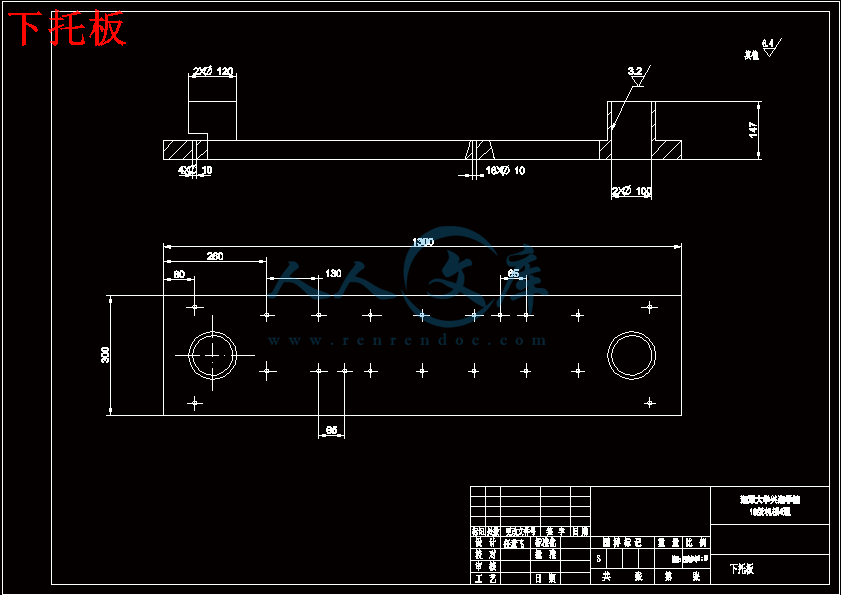
下托板.dft
下托板.dwg
任务书.doc
外文翻译--部分频谱与齿轮缺陷发现相互关系的实际应用.doc
总装配.dwg
横梁.dft
横梁.dwg
横梁固定件.dft
横梁固定件.dwg
牌坊架.dft
牌坊架.dwg
皮革剪板机设计说明书.doc




目录
摘要………………………………………………………………………………………1
1 绪论……………………………………………………………………………………3
1.1 研究的背景、目的和意义…………………………………………………………3
1.2 剪板机的分类及应用………………………………………………………………3
1.3 设计的意义…………………………………………………………………………4
1.4 剪板机设计步骤……………………………………………………………………5
2 皮革剪板机总体结构…………………………………………………………………6
2.1 皮革剪板机设计要求………………………………………………………………6
2.2 配个剪板机总体布局………………………………………………………………6
2.3 主要部件的设计……………………………………………………………………7
3 剪板机基本性能参数…………………………………………………………………10
3.1 剪切力确定…………………………………………………………………………10
3.2 压料力的确定………………………………………………………………………11
3.3 剪切角的确定………………………………………………………………………11
3.4 上刀片的行程量……………………………………………………………………12
4 剪板机机械设计………………………………………………………………………13
4.1 整体设计……………………………………………………………………………13
4.2 机架…………………………………………………………………………………15
4.3 刀架…………………………………………………………………………………16
4.4 刀具…………………………………………………………………………………18
5 液压部分设计…………………………………………………………………………20
5.1 基本方案……………………………………………………………………………20
5.2供油方式卸荷回路…………………………………………………………………21
5.3 液压系统性能的验算………………………………………………………………23
5.4 液压系统的调试……………………………………………………………………29
5.5 液压系统的维护及注意事项………………………………………………………30
6 结论……………………………………………………………………………………32
参考文献…………………………………………………………………………………33
摘 要
本文设计了一台简易剪板机,能够实现对厚度10mm,宽度700mm行剪切,剪断时间小于10s,重点就机架、刀架等重要部件进行了设计,在设计中通过对比国内外剪板机,力求设计出结构简单,操作简便,同时经济、合理的剪板机,具体设计思路上:减少了剪切的时间并且提高了剪切精度。采用人工送料以降低成本。近年来,随着模具技术和冲压技术的发展,剪板机的应用范围在不断地扩大,数量在不断地增加。预计不久的将来,剪板机在冲压用剪板机中的比例将会愈来愈大。
关键词 机架; 刀架; 剪切精度
Abstract
This text designed to the infrastructure design of guillotine shear, can carry out to shear to slice the plank material thickness 10 mm, the width 700mm, clipping time is smaller than 10 second, the point carried on a design for the parts with important etc. of the machine, knife and passed contrast to the infrastructure design of guillotine shear at home and abroad in the design and tried hard for to design structure simple, operate simple, economic in the meantime, reasonable of the infrastructure design of guillotine shear, for the put type knife formely and connect the pole type knife carried on innovation: consumedly reduced to shear to slice of time and raised to shear to slice accuracy.In recent years, along with molding tool technique and hurtle to press a technical development, the infrastructure design of guillotine shear at constantly extension, amount at constantly increment.Anticipate near future, the infrastructure design of guillotine shear at blunt press to use to shear the comparison in the infrastructure design of guillotine shearr will be bigger and bigger.
Keywords Machine;Knife;hear to slice accuracy.
绪 论
研究的背景、目的和意义
随着我国制造业的发展,剪板机床的发展越来越成为机械制造行业的中流砥柱,通用型高性能剪板机,广泛适用于航空、汽车、农机、电机、电器、仪器仪表、医疗器械、家电、皮具、五金等行业。
锻压机械是指在锻压加工中用于成形和分离的机械设备,1842年,英国工程师史密斯创制第一台蒸汽锤,开始了蒸汽动力锻压机械的时代。1795年,英国的布拉默发明水压机,但直到19世纪中叶,由于大锻件的需要才应用于锻造。随着电动机的发明,十九世纪末出现了以电为动力的机械剪板机和空气锤,并获得迅速发展。二十世纪初,锻压机械改变了从19世纪开始的向重型和大型方向发展的趋势,转而向高速、高效、自动、精密、专用、多品种生产等方向发展。于是出现了每分种行程2000次的剪板机。所谓剪板机一般是指每分钟的行程次数为普通剪板机的5—10倍的剪板机。剪板机是带有自动送料装置,可完成板料高效率、精密加工的机械剪板机,具有自动、高速、精密三个基本要素。
近十多年来,随着对发展先进制造技术的重要性获得前所未有的共识,冲压成形技术无论在深度和广度上都取得了前所未有的进展,其特征是与高新技术结合,在方法和体系上开始发生很大变化。计算机技术、信息技术、现代测控技术等冲压领域的渗透与交叉融合,推动了先进冲压成形技术的形成和发展。 冷冲压生产的机械化和自动化,为了满足大量生产的需要,冲压设备已由单工位低速剪板机发 展到多工位剪板机。一般中小型冷冲件,既可在多工位剪板机上生产,也可以在剪板机上采用多工位级进模加工,是冷冲压生产达到高度自动化。
在汽车、航空航天、电子和家用电器领域,需要大量的金属板壳零件,特别是汽车行业要求生产规模化、车型个性化和覆盖件大型一体化。进入21 世纪,我国汽车制造业飞速发展,面对这一形势,我国的板材加工工艺及相应的冲压设备都有了长足的进步。
1.2剪板机的分类及应用
剪板机属于直线剪切机类,主要用于剪裁各种尺寸金属板材的直线边缘。在轧钢、汽车、飞机、船舶、拖拉机、桥梁、电器、仪表、锅炉、压力容器等各个工业部门中有广泛应用。
剪板机种类较多,按其工艺用途和结构类型可以分为:
1.平刃剪板机 剪切质量好,扭曲变形小,但剪切力大,耗能大。机械传动的较多。该剪板机上下两刀刃彼此平行,常用于轧钢厂热剪切初轧方坯和板坯;按其剪切方式又可分为上切式和下切式。
2.斜刃剪板机剪板机的上下两刀片成一个的角度,一般上刀片是倾斜的,其倾斜角一般为1°~6°。斜刃剪板机剪切力比平刃剪板机小,故电机功率及整机重量等大大减小,实际应用最多,剪板机厂家多生产此类剪板机。该类剪板机按刀架运动形式分闸式剪板机和摆式剪板机;按主传动系统不同分为液压传动和机械传动两类。
3.多用途剪板机:
(1)板料折弯剪切机:即在同一台机械上可完成剪切和折弯两种工艺。
(2)联合冲剪机:即可完成板材的剪切,又可对型材进行剪切,多用于下料工序。
4.专用剪板机:
(1)板材开平线剪板机:用于板材开卷校平线上,为配合生产线速度快剪切要求而设计的高速剪板机,厚板线上多为液压高速剪板机,薄板线上多配气动剪板机;高速线上配有飞剪机,连续生产,效率高。
(2)钢结构生产线剪板机:多用于角钢、H型钢自动生产线完成剪断工序。
(3)冷弯成型线剪板机:例如汽车纵梁冷弯线、车厢侧挡板生产线、彩钢板成型线等生产线上配置的专用剪板机等。
1.3设计的意义和设计步骤
毕业设计和毕业论文是本科生培养方案中的重要环节。学生通过毕业论文,综合性地运用几年内所学知识去分析、解决一个问题,在作毕业论文的过程中,所学知识得到疏理和运用,它既是一次检阅,又是一次锻炼。通过这次检验,不但可以提高学生的综合训练设计能力、科研能力(包括实际动手能力、查阅文献能力,撰写论文能力)、还是一次十分难得的提高创新能力的机会,并从下个方面得到训练:
1.学会进行方案的比较和可行性的论证;
2.了解设计的一般步骤;
3.正确使用各种工具书和查阅各种资料;
4.培养发现和解决实际问题的能力。
利用所学的机械各方面的知识,我选择这个课题为我的毕业设计,进行大胆的尝试。设计中主要以课本和各种参考资料作为依据,从简单入手,循序渐进,逐步掌握设计的一般方法,把所学的知识形成一个整体,以适应以后的工作需要。当然,初次设计,知识有限,经验不足,一些问题考虑不周,也可能存在有某些错误和遗漏,恳请各位老师批评指正。
剪板机是各类机械产品的一种,设计时着手于其原理和主要部件的计算校核,了解剪板机的工作状态,以此为基础设计刀架、机架等各类零部件,液压部分可以采用简单的单缸液压系统,主要考虑保证液压平衡性能。
1.3 剪板机设计步骤
设计中一般采用三阶段法,即总体设计、部件设计和零件设计或者初步设计、技术设计与工艺设计。在实验设计与计算机辅助设计(CAD)中,多采用既分阶段又与平行兼顾的设计,以便相互协调.
总体设计程序为:
1.明确设计思想
2.分析综合要求
3.收集资料、对剪板机进行学习研究
4.设计剪板机总体方案
5.对剪板机各零件进行三维建模
6.剪板机总体三维图,并导出工程图
7.画出剪板机主要零件图
8.撰写设计说明书。
2 皮革剪板机总体结构
2.1皮革剪板机设计要求
设计要求是进行每项工程设计的依据。在制定基本方案并进一步着手剪板机各部分设计之前,必须把设计要求以及与该设计内容有关的其他方面了解清楚。
1.主机的概况:用途、性能、工艺流程、作业环境、总体布局等;
2.剪板机的工作过程及其各部件的配合形式;
3.各动作机构的载荷大小及其性质;
4.对调速范围、运动平稳性、转换精度等性能方面的要求;
5.对防尘、防爆、防寒、噪声、安全可靠性的要求;
6.对效率、成本等方面的要求。
2.2 皮革剪板机总体布局
剪板机的总体布局是设计剪板机时影响全局性的决策部署。在总体布局确定后,才能确定部件之间的相对位置及运动关系,进一步具体设计剪板机。总体布局的影响是多方面的,其中,刀具的剪切轨迹是首要决定的。刀具的剪切轨迹确定后,剪板机的布局、传动、结构及外形等就可以初步决定。被加工工件的尺寸、重量和技术要求与剪板机的布局有密切关系。总体布局还需要考虑人的因素,能够满足操作要求,必须有利于减轻操作者的劳动强度,以提高工作
参考文献
1、刘灏 机械设计手册 北京; 机械工业出版社,2002
2、朱龙根 简明机械零件设计手册 北京; 机械工业出版社,2004
3、吴宗泽 罗圣国 机械设计课程设计手册 北京; 高等教育出版社,1992
4、郭爱莲 新编机械工程技术手册 北京; 经济日报出版社,1991
5、林石 剪切机设计计算方法(一)、(二) 机械工业出版社,2003
6、洪得纯 于志宏 祝悦红 国外锯切机的新进展 吉林; 吉林林学院1994
7、王知行 刘廷荣 机械原理 北京; 高等教育出版社,2000
8、南京林业大学主编 木材切削原理与刀具 北京; 中国林业出版社,1997
9、庞庆海 剪板机械设备 北京; 化学工业出版社,2005
10、孙桓 陈作模 机械原理 北京; 高等教育出版社,2001
11、濮良贵 纪名刚 机械设计 北京; 高等教育出版社,2001
12、王世刚 张春宜 徐起贺 机械设计实践 哈尔滨; 哈尔滨工程大学出版社,2001
13、张慧光 剪板机设计 沈阳; 沈阳锻压机床厂,1978
14、王三民 诸文俊 机械原理与设计 北京; 机械工业出版社,2000
15、姜继海 宋锦春 高常识 液压与气压传动 北京; 高等教育出版社,2000
16、李兴中 陈启松 朱福元 液压设备管理维护手册 上海; 上海科学技术出版社,1996
17、单丽云 工程材料 徐州; 中国矿业大学出版社,2000
18、丁德全 金属工艺学 北京; 机械工业出版社, 2000
 川公网安备: 51019002004831号
川公网安备: 51019002004831号