防抱死制动系统的执行部件设计
乘用车防抱死制动系统的分析及其关键部件的设计初步【优秀】【带SW三维图及仿真】【word+5张CAD图纸全套】【毕业设计】
【带任务书+开题报告+鉴定意见+评阅表+中期检查表+外文翻译+答辩ppt】【30页@正文16300字】【详情如下】【需要咨询购买全套设计请加QQ1459919609】.bat
solidedge st4 建模
中期检查表 .doc
任务书.doc
制动器运动仿真.flv
外文文献.pdf
外文文献翻译.doc
开题报告.doc
弹簧A4.dwg
总装图纸A0 .dwg
支撑架A2.dwg
正文.doc
浮动钳盘工作动画.swf
盘体A0.dwg
盘式制动器工作原理 .swf
答辩.ppt
评阅表.doc
鉴定意见表.doc
钳体A2.dwg
钳盘式制动器标准.pdf
附件资料
任务书
论文(设计)题目: 乘用车防抱死制动系统的分析及其关键部件的设计初步
一、主要内容及基本要求
查阅相关文献资料,了解乘用车防抱死制动系统的国内外研究动态,完成乘用车防抱死制动系统的分析及其关键部件的设计初步。
要求:
1、查阅相关资料,基本掌握乘用车防抱死制动系统的组成及功能;基本掌握实时道路识别技术。
2、设计一款结构简单、可靠的防抱死制动系统的执行部件。
3、不少于2*A0图纸;
4、撰写毕业设计说明书。
5、相关外文文献翻译,字数3000字以上。
二、重点研究的问题
防抱死制动系统的执行部件设计
三、进度安排
序号各阶段完成的内容完成时间
1查阅资料、调研第1-2周
2开题报告、制订设计方案第3周
3方案(设计)第4-5周
4防抱死制动系统的执行部件设计第6-7周
5写出初稿,中期检查第8-9周
6修改,写出第二稿 第10-11周
7写出正式稿 第12-13周
8答辩第14周
四、应收集的资料及主要参考文献
张秀芹.多轴车ABS制动性能仿真与试验研究[D].武汉理工大学,2012.
贾玉梅.汽车ABS虚拟仿真平台的研究与应用[D].重庆邮电大学,2011.
李文娟,付天雷,陈凤林等.汽车防抱死制动系统的自寻最优控制[J].哈尔滨理工大学 学报,2010.
郝茹茹,赵祥模,周洲等.整车防抱死制动系统台架检测与道路对比试验[J].农业机械 学报,2013.
目录
摘要I
ABSTRACTI
第1章 绪论1
1.1 防抱死制动系统的研究意义1
1.2 国外研究动态1
1.3 国内ABS研究动态2
1.4 ABS系统的设计要求3
1.5 ABS系统的质量准则3
1.6 主要评价指标4
1.7 ABS的展望4
1.8 完成的内容及设计的创新之处5
1.9 研究的主要方法5
第2章 ABS的基本结构和工作原理6
2.1 ABS 的基本分类6
2.2 ABS基本组成及工作过程6
2.3 ABS的执行机构8
第3章 制动器的设计初步10
3.1 盘式制动器的初步了解10
3.2 盘式制动器的机构及其特点10
3.3 制动系统的技术参数及要求11
3.4 浮动钳盘式制动器的设计流程12
3.5 参数的选择12
3.6 摩擦衬块的磨损特性计算13
3.7 比滑磨功的核算14
3.8 制动器的热容量和温升的核算15
3.9 盘式制动器制动力矩的计算16
第4章 盘式制动器主要零部件的结构设计17
4.1 制动盘17
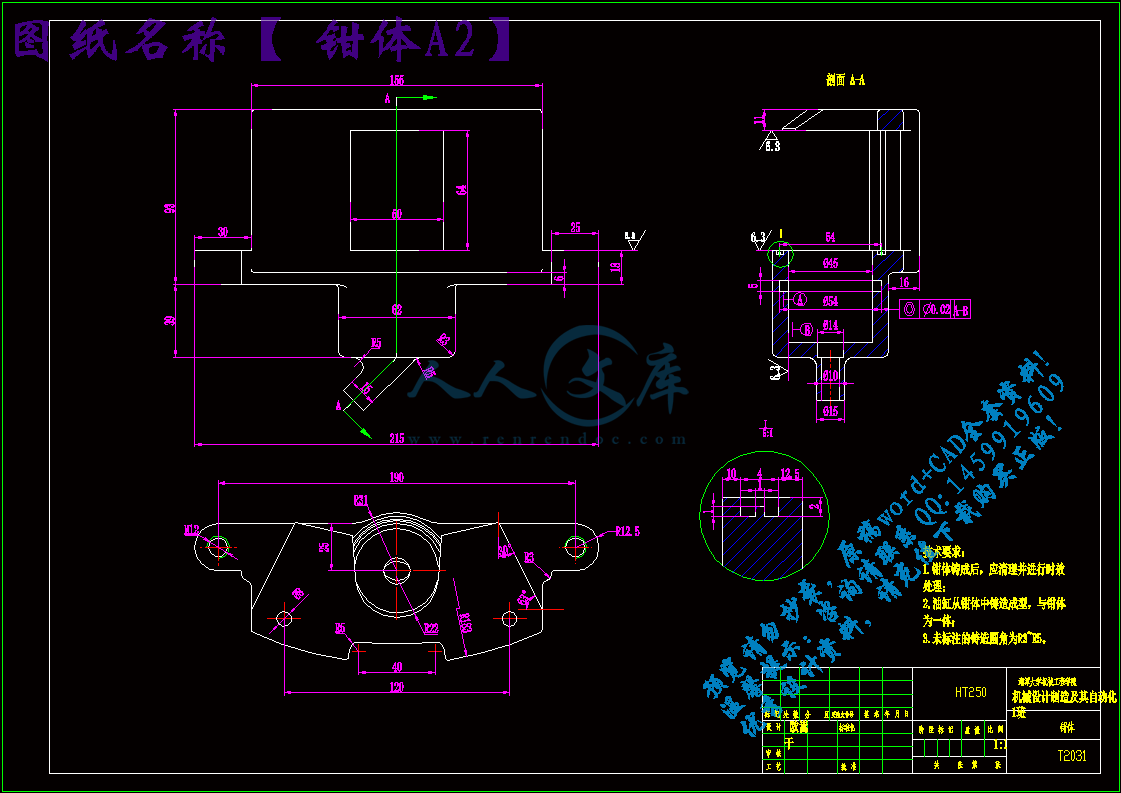
4.2 制动钳18
4.3 制动块19
4.4 摩擦材料20
4.5 制动性能评价指标21
总结23
参考文献24
附录A 外文翻译25
附录B 盘式制动器零件图及装配图43
乘用车防抱死制动系统的认识及其盘式制动器的设计初步
摘要
ABS是英文Anti-lock Brake Syetem的缩写,全文的意思是防抱死制动系统,它作为一种具有防以及防锁死等功能的汽车主动安全控制系统,已被广泛运用于汽车上。ABS主要由微机控制单元(ECU)、车轮转速传感器、制动控制电路和制动压力调节装置等部分组成。汽车在制动过程中,ABS系统能使车轮处于非抱死状态,从而可以防止车辆的甩尾和侧滑,提高了汽车制动过程的方向稳定性。
本文介绍乘用车防抱死制动系统的国内外研究动态,对乘用车防抱死制动系统的工作原理进行分析,解析其基本组成。车轮制动器作为行车制动系的重要组成部件,本次论文将重点研究盘式制动器的制动原理,对ABS的执行制动部件进行合理性探讨,在散热性能及其结构上对盘式制动器进行创新设计和改良。最后通过三维制图软件画出装配图和零件图以更充分地表达设计理念。
关键词:ABS系统 ABS工作原理 基本组成 盘式制动器 结构设计
Understanding and design of passenger car disc brake anti-lock braking system initially
ABSTRACT
ABS is Anti-lock Brake Syetem English abbreviation, the full text mean anti-lock braking system, which as well as having an anti-anti-lock function of vehicle active safety control system has been widely used in the car. ABS Main components of the computer control unit (ECU), a wheel speed sensor, the brake control circuit and the brake pressure regulating devices. Car during braking, ABS system allows the wheels in a non-locking state, which can prevent the vehicle from skidding flick and improves directional stability during braking of the car.
This article describes the passenger anti-lock braking system dynamics studies abroad, for passenger anti-lock braking system works to analyze, parse its basic components. As an important component of the wheel brake components brake system. This paper will focus on the principles of the brake disc brakes, brake parts for ABS implementation of rational discussion on the thermal structure of the disc brake performance is extremely innovative design and improvement. Finally, three-dimensional mapping software to draw assembly drawings and part drawings to more fully express the design concept.
Keyword :Anti-lock Brake Syetem ; ABS system works basically;
The basic composition ; Disc brakes ;Structural design
第1章 绪论
1.1 防抱死制动系统的研究意义
安全,环保和节能是当前汽车技术发展的三大主题。人们在享受车轮上的世界时,汽车的安全也是人们一直在探讨的话题。我国已不知不觉步入了汽车社会,汽车乃是当今中国最主流的交通工具。然而据公安部统计,2010年和2011年,在全国道路交通事故死去的人,数量分别达到了65225和62387,该数字已经连续十余年保持世界首位,车祸已成为中国社会之患。统计发现,汽车紧急制动时发生侧滑或制动距离过长等情况往往是导致重大的道路交通事故的发生的原因。汽车的制动性能已经成为了评价汽车主动安全性的一个非常重要的指标。研究和改善汽车的制动性能有着很大的价值。以ABS刹车防抱死系统为例,如果汽车前轮抱死,车辆将失去方向控制能力,不能实现弯道转向;如果后轮抱死,车辆将发生方向稳定性,发生侧滑或甩尾危险现象。汽车安装ABS后,可以大大缩短刹车距离并且在刹车过程中保持汽车方向可控制,以避免碰撞损伤。总体来看,ABS系统有三大优点:
1.能够增加汽车制动时的方向稳定性。
在汽车制动过程中,作用在四个轮子上的制动力往往是是不相等的,如果汽车的前轮出现抱死现象,汽车的行驶方向就无法得到控制,这将极大可能造成非常危险的后果;如果汽车的后轮出现抱死现象,则会出现侧滑、甩尾的严重事故,更有甚者会使汽车整个掉头。ABS制动系统可以防止汽车制动时车轮被完全抱死,提高汽车制动的方向稳定性。研究数据表明,装有ABS制动系统的车辆,可以将因车轮侧滑,甩尾等引起的道路交通事故比例降低8%左右。
2.能缩短制动距离。
研究表明,在同样紧急制动的情况下,防抱死制动系统可以将滑移率控制在20%左右,这样,汽车可获得最大的纵向制动力,起到缩短制动距离的效果。
3. 改善了汽车轮胎的磨损状况,防止出现爆胎情况。
事实上,车轮抱死会造车轮轮胎局部急剧磨损,降低轮胎使用寿命。
1.2 国外研究动态
ABS装置最早应用在铁路上,在20世纪30年代,德国﹑美国﹑法国等国家提出有关防抱死装置专利的申请,而根据官方记录,最早的汽车防抱死系统是1932年英国人申请的专利“制动时防止车轮压紧转动车轮的安全装置”,该专利号为382241。直到20世纪50年代,ABS才开始应用于汽车工业。1908年,一位叫J. E. Francis的英国工程师提出了关于“铁路车辆车轮抱死滑动控制器”的有关理论,但这些理论实际上无法实用化。在接下来的30年中,包括Richard Trappe的“车轮抱死防止器”、Werner Mhl的“液压刹车安全装置”与Karl Wessel的“刹车力控制器”等尝试都以失败告终。20世纪50年代,Good Year航空公司开始尝试把飞机用ABS应用在载货汽车上,并开发出独具特点的ABS装置,这一时期初期电子计算技术开始应用到ABS装置中。1954年,美国福特汽车公司将法国生产的名航机用ABS装置装用在了林肯牌轿车上。虽然这些尝试都以失败告终,但为汽车应用ABS留下了很好的经验。经过人们长期的努力与尝试,1958年Dounlop公司开发出了 应用在载货车的车用ABS。1968年,美国福特公司与Keslsey Hayes公司合作并最终成功开发了车用ABS装置。随着电子技术的飞速发展,20世纪70年代末,欧洲开始批量生产应用于轿车和商用汽车的ABS系统。进入20世纪80年代末,ABS的发展速度变得越来越快。在发展过程中,ABS的体积不断减少,重量也不断地减轻,其控制盒故障诊断功能也越来越完善。在欧洲,美国和日本等国家,ABS应用在汽车上越来越普及,欧洲和美国在法规的要求下,ABS装车率达到100%。随着计算机技术以及新技术新材料的不断出现,人们开始尝试将ABS﹑4WS和DYC技术结合在一起,在ABS原有的基础上,发展防滑控制系统(ASR)﹑电子制动控制系统(EBS)及车辆动力学控制系统(VDC)。四轮转向技术4WS(Four Wheer Steering)是主动底盘控制的重要组成部分,主要是用来改善汽车操纵稳定性。在国外4WS有着很好的发展前景。相比4WS技术,DYC则对汽车有更高的稳定性控制能力。DYC是Direct Yaw Moment Contrl的缩写,称为横摆力矩控制。20世纪90年代末,本田汽车工程师Shibahata就由轮胎侧向力产生的横摆力矩是如何随汽车质心侧偏角的变化而变化作出了相关讨论。目前,世界第一大ABS装置生产厂家――德国Bosch(博世)公司生产的ABS装置已被广泛用于大众,宝马,通用和奥迪等公司的各系列车型中。此外,日本也生产了大量的ABS装置,广泛安装在本田,日产,丰田及马自达等车系上。
1.3 国内ABS研究动态
我国ABS 的研究起步比较晚。上世纪80 年代初,诸如东风汽车公司、上海汽车制动有限公司、山东重汽集团和重庆公路研究所等企业,还有吉林大学和清华大学等高校开始从事ABS的研制工作。其中清华大学率先搭建了汽车安全与节能国家重点实验室,该实验室在宋健,欧阳明高等多名博导和教授的带领下拥有着很强的科技研发实力, 他们在国内开展了有关汽车碰撞安全的课题研究,自行设计建成了测试分析处理系统和汽车碰撞试验台,这些成果填补了国内在测试分析技术和碰撞试验研究方面的空白,在国内率先开展汽车侧面碰撞、行人碰撞及正面碰撞等安全性研究,形成了一套比较系统的设计理论和方法。该室引进和开发一些先进的仪器设备,比如FEV控制器仿真系统﹑汽车力学参数综合试验台、模拟人及标定试验台、电液振动台、Kodak 高速图像运动分析系统、发动机排放分析仪、ABS车载数据采集系统、发动机电控系统开发装置及工况模拟器、转鼓试验台、汽车底盘测功机、噪声测试系统、汽车操纵稳定性测试仪、汽车弹射式碰撞试验台及翻转试验台、电动车蓄电池试验台、电机及其控制系统试验台等。针对ABS该实验室做了许多方面的研究和探索,比如,在ABS 控制量、轮速信号异点剔除、轮速信号抗干扰处理以及防抱死电磁阀动作响应研究等领域的研究都处于国内领先的地位。吉林大学的汽车动态模拟国家重点实验室,该实验室在轮胎力学模型,人车闭环操作仿真以及汽车操纵稳定性等方面的研究成果均处在世界领先地位。有郭孔辉教授领导的研究小组设计并开发了具有自主知识产权的大型试验设备——平板式轮胎力学特性试验台,该试验台为轮胎力学特性的理论研究和试验研究起到了积极的推动作用。西安的博华公司生产的BH1203-FB型ABS和BH1101-FB型ABS被认为到达了国内领先水平。
1.4 ABS系统的设计要求
一般把转向能力,稳定性和最佳制动距离作为评价ABS的主要指标。一般对ABS的设计能满足以下的要求 :
1)在调节制动过程时,汽车行驶稳定性和转向能力必须得到保证;
2)即使在各个车轮上的附着力系数不相等,不可避免的转向反应也应该尽可能小;
3)必须在汽车的整个速度范围内进行调节;
4)调节系统应该最大程度上利用车轮在路面上的附着性,这时优先考虑保持转向能力,然后再保障缩短制动距离的要求
5)调节装置应该能够快速地适应来自路面传递能力的变化
6)在波状路面上给以任意的强迫制动,汽车都应能被完全地控制住;
7)调节装置必须能够对出覆水路面做出识别,并能对此作出正确的反应;
8)调节装置只能附加在常规制动装置上
9)所有的这些对调节装置的要求,汽车轮胎在路面上行驶时都必须得到满足
1.5 ABS系统的质量准则
每一种ABS产品的出现都是为了能投入市场,应用于实际。ABS产品想要开拓市场,它必须具有高的可靠性能。ABS产品的可靠性必须能够满足苛刻的汽车使用条件的要求。评价一个ABS系统应该遵循的质量准则有以下几点 :
(1)保证良好的行驶稳定性
(2)转向能力满足汽车安全行驶要求
(3)高附着力系数的利用率
(4)舒适性良好
1.6 主要评价指标
对ABS系统性能的评价必须是要综合各项指标,ABS的性能好坏最终是要通过道路试验来验证。每一种ABS产品都必须要通过严格的试验检测后才可以进行装车使用。评价ABS系统主要有以下几个指标 :
(1)良好的抗外界电磁场干扰的能力
(2)基本功能(保证制动车轮不抱死)
(3)附着力系数利用率
(4)对道路条件突变的适应性
(5)当产生电器故障可自行解除ABS的工作
1.7 ABS的展望
ABS在汽车上的成功应用,说明了防抱死理论的可行性。虽然说ABS的理论及其总体结构方案已趋于成熟,但是随着道路升级以及汽车技术的发展和普及,人们对汽车行驶制动安全性的要求越来越高。国内外的一些研究动态以及高档轿车的实际应用情况表明,ABS技术将会在着以下几个方面进行拓宽发展 :
1.自身控制技术的提高。随着计算机技术的发展,ABS向纵深扩展,比如驱动防滑装置,简称ASR(Anti-slip-regulation)及速度限制器等。基于滑移率的控制算法也有了十分明确的理论指导。在控制生产成本的前提下,ABS防抱死系统将向体积更小,性能更可靠以及功能更加全面实用的方向发展。
2.把ABS和驱动防滑控制装置ASR结合在一起,实现一体化。当汽车行驶时车轮出现滑动现象时,实际上会出现以下两种情况:一种情况是汽车在制动时车轮出现抱死而产生的车轮滑移现象;另一种是车身不动但车轮仍在转动,或者说是汽车的运动速度比转动车轮的轮缘速度小,我们称之为滑转。通常ABS是以防止车轮抱死为目的,而ASR则是为了防止车轮出现过分滑转的现象;ABS的作用是为了缓解制动,而ASR则是对车轮施加制动力。由于这两种装置在技术上比较接近,并且都能在低附着性的地面上充分体现出它们的作用,所以人们将二者有机地结合起来。
3.车辆动力学控制系统VDC(Vehicle Dynamics Control)或电子稳定控制ESP。VDC主要在ABS/ASR基础上通过测量方向转盘,侧向加速度和横摆角速度对车辆的运动状态进行控制。设计车辆动力学控制系统的目的是为了解决汽车转向行驶时出现的方向稳定性问题。能保证车辆处于危险情况下实现自动控制。
4.ABS/ASR与自动巡航系统ACC(Adaptive Cruise Control)集成。作为汽车主动安全的一项新技术,ACC装置能够是汽车主动避免碰撞。ABS/ASR和ACC的运作都是建立在相同的发动机调节装置,制动力调节装置以及轮速采集系统上,因此,把ABS和ACC结合在一起将提高汽车安全性的的同时,会大大降低生产成本。
5.将ABS与电子机械制动EMB结合,或者与电子液压制动EHB结合后,ABS就会有更快的的响应速度,表现出更好的控制效果,而且更容易与其它电子系统实现集成,这也将是在ABS的基础上开发或添加其它制动系统的一个趋势。
6.把电子制动力分配装置(EBD)嵌入到ABS系统中,则构成了ABS+EBD系统。在汽车开始制动压力调节之前,EBD能够高速地计算出汽车四个轮胎与路面间的附着力大小,然后调节各个车轮与附着力的关系,使二者能匹配,更大程度地提高车辆制动时的稳定性能,同时也尽可能地达到缩短制动距离的效果。
1.8 完成的内容及设计的创新之处
本次完成的任务主要是对乘用车防抱死制动系统的工作原理进行了分析,解析其基本组成,掌握汽车防抱死制动工作原理。对ABS的执行制动部件进行合理性探讨,重点研究了盘式制动器的结构,在散热性能及其结构上对盘式制动器进行创新设计和改良。最后通过三维制图软件画出装配图和零件图。完成相关外文文献的翻译。
主要的创新点有:(1)制动盘除了采用盘式通风孔设计,还对通风道的位置做了特殊要求,改善其散热性能;(2)改变原有的保持弹簧形状,设计一款安装定位准确且便于安装的保持弹簧;(3)在结构上对防尘油套进行改进,使其与制动钳嵌合,提高油缸防尘防污能力。
参考文献
[1]张秀芹.多轴车ABS制动性能仿真与试验研究[D].武汉理工大学,2012.
[2]贾玉梅.汽车ABS虚拟仿真平台的研究与应用[D].重庆邮电大学,2011.
[3]李文娟,付天雷,陈凤林等.汽车防抱死制动系统的自寻最优控制[J].哈尔滨理工大学 学报,2010:16-20.
[4]郝茹茹,赵祥模,周洲等.整车防抱死制动系统台架检测与道路对比试验[J].农业机械 学报,2013:12-17.
[5]齐晓杰主编.制动系统[M].北京:化学工业出版社,2005.
[6]马保吉,朱均.盘式制动器制动过程能量分析[J].机械科学与技术,1998:6-9.
[7]刘惟信编.汽车制动系的结构分析与设计计算[M].北京:清华大学出版社,2004.
[8]李果编著.车辆防抱死制动控制理论与应用[M].北京:国防工业出版社,2009.
[9]周志立等编著.汽车ABS原理与结构[M].北京:机械工业出版社,2005.
[10]周良德,杨世平.现代工程图学[M].湘潭:湖南科学技术出版社,2007.
[11]董鹏.盘式制动器及其与整车匹配的研究[D].武汉理工大学,2012.
[12]杨晓明等.盘式制动器的全性能优化设计[J].中国机械工程 第16卷第7期,2005.
[13]喻凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005.
[14]王望予主编.汽车设计[M].北京:机械工业出版社,2007.
[15]濮良贵,纪明刚主编.机械设计[M],8版.北京:高等教育出版社,2006.






 川公网安备: 51019002004831号
川公网安备: 51019002004831号