人人文库网 > 图纸下载 > 毕业设计 > 中厚板板形仪长度检测系统设计【含全套CAD图纸】【答辩毕业资料】

毕业论文.doc

中厚板板形仪长度检测系统设计【含全套CAD图纸】【答辩毕业资料】

资源目录

CAD 中厚板板形仪长度检测系统设计.rar

CAD 中厚板板形仪长度检测系统设计

A3激光测速仪位置安装.dwg---(点击预览)

A3 轴.dwg---(点击预览)

A3 热轧无缝钢管.dwg---(点击预览)

A3 激光传感器局部位置安装.dwg---(点击预览)

A3 护栏.dwg---(点击预览)

A3 GY4型凸缘联轴器.dwg---(点击预览)

a2 龙门横梁架.dwg---(点击预览)

a2 扶梯.dwg---(点击预览)

A1 辊道装配图.dwg---(点击预览)

A0 中厚板板形仪总装图.dwg---(点击预览)

PDF

A3激光测速仪位置安装-Model.pdf---(点击预览)

A3 轴-Model.pdf---(点击预览)

A3 热轧无缝钢管-Model.pdf---(点击预览)

A3 激光传感器局部位置安装-Model.pdf---(点击预览)

A3 护栏-Model.pdf---(点击预览)

A3 GY4型凸缘联轴器-Model.pdf---(点击预览)

a2 龙门横梁架-Model.pdf---(点击预览)

a2 扶梯-Model.pdf---(点击预览)

A1 辊道装配图-Model.pdf---(点击预览)

A0 中厚板板形仪总装图-Model.pdf---(点击预览)

压缩包内文档预览：(预览前20页/共49页)

编号：346957 类型：共享资源大小：42.13MB 格式：RAR 上传时间：2014-10-22 上传人：好资料QQ****51605 IP属地：江苏

45
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: cad 厚板板形仪长度检测系统设计

资源描述：

【温馨提示】购买原稿文件请充值后自助下载。

[全部文件] 那张截图中的文件为本资料所有内容，下载后即可获得。

预览截图请勿抄袭，原稿文件完整清晰，无水印，可编辑。

有疑问可以咨询QQ：414951605或1304139763

全部文件包含以下内容

全部文件.jpg

A0 中厚板板形仪总装图.gif

A1 辊道装配图.gif

a2 扶梯.gif

a2 龙门横梁架.gif

A3 GY4型凸缘联轴器.gif

A3 护栏.gif

A3 激光传感器局部位置安装.gif

A3 热轧无缝钢管.gif

A3 轴.gif

A3激光测速仪位置安装.gif

摘要
中厚板（厚度为的钢板）是我们日常工业加工中经常用到的一种基础材料，它在工业生产中需求量非常大，起着中流砥柱的作用。所以我们对中厚板的质量要求有了很高的标准，其中包括对它进行尺寸测量如：长度，宽度和平坦度等。长度是中厚板轧制产品的一项关键的质量指标，对轧制生产线、产品的应用都有很大的影响。近年来，随着我国现代化的不断发展，我们对钢材的需求量以及品质感也提出了更高的要求。长度检测系统为后续一系列钢板检测系统提供关键的数据支撑，将会直接影响到后期产品的质量。由于冷轧中厚板在辊道上的输送速度是轮廓检测过程中的一个非常关键的数据，因此对速度的测量精度直接关系到轮廓检测的准确程度。本论文研究的是采用一种新型的非接触式测速方法与传统的测量方法有很大不同。钢板长度是通过多普勒激光测速仪得到速度，依据一段时间内测量的速度来计算钢板的长度。求得各个纬度的长度，平均长度，最大长度和最小长度。由于条件所限，实验主要采用Labview软件构建整个系统的检测程序。随着系统的运行能立即得出所需要的关键数据以便用来分析。以下是论文的详细内容：
第1章本章主要是介绍中厚板及板形仪的定义。国内外中厚板板形仪的研究现状和发展趋势，以及中厚板长度检测的研究意义和价值。根据其发展现状和研究的重要性，设计一套完整的长度检测系统。
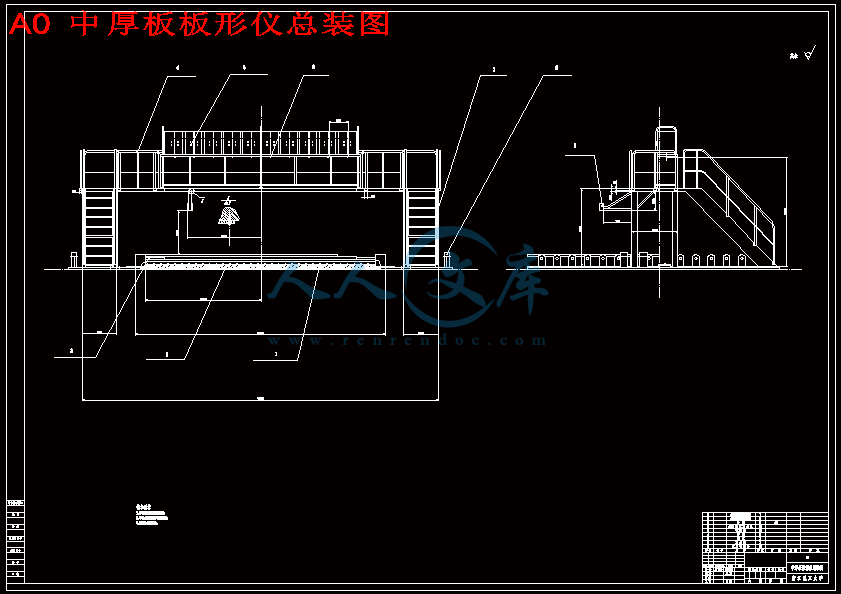
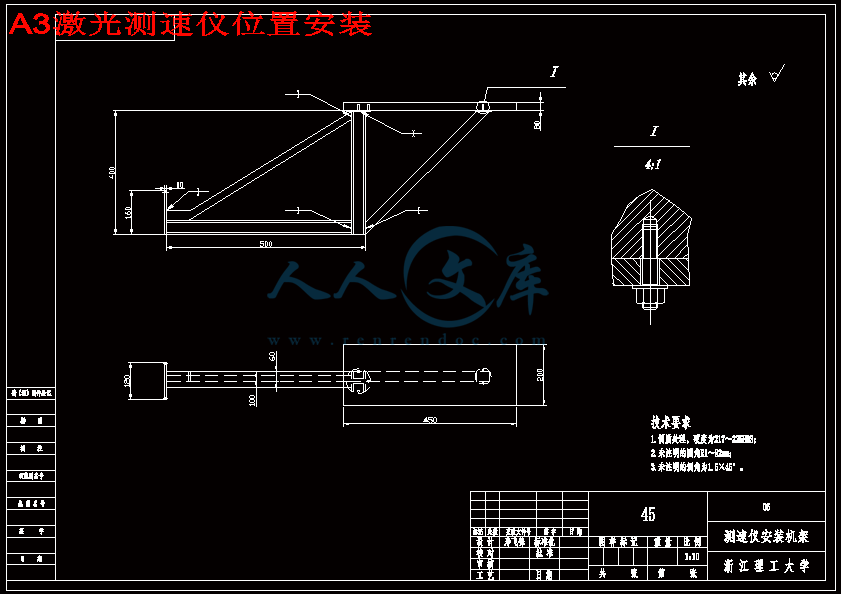
第2章本章根据研究所需设计检测仪系统的整体构架，其中包括传感器，多普勒测速仪的位置安装定位。重点介绍长度检测系统的工作原理。
第3章本章论述检测系统的组成和相关参数，着重介绍多普勒激光测速仪工作原理。
第4章本章主要介绍运用Labview构建程序框图和前面板。通过运行虚拟程序得到相应数据，并对数据进行分析。
第5章使用Matlab软件编写程序用来处理测量所得数据。
第6章本章主要是总结研究过程中所遇到的问题和对构建的程序框图所产生的一些不足，提出解决之道和展望未来研究方向。

关键词：长度检测多普勒测速程序框图总结

Abstract
Steel plate is often used as a base material in our industrial process .We need a great quantity numbers. It plays a very important role. So we want have the quality of steel plate by a very high standard. Include its size measurement such as length, width and flatness, etc. The length is a key quality indicator, has a significant impact in production lines and product application. In recent years, with the continuous development of China's modernization, Demand for steel plate and a sense of quality we also put forward higher requirements. Length detection system give the follow-up series of steel plate detection system provides key data support will directly affect the latter part of the quality for the product. Cold-rolled plate in the conveying speed of the rollers is a very critical detection process data, the accuracy of speed measurement is directly affects the accuracy of the contour detection. This study is the use of a new type of non-contact speed is very different from the traditional measurement methods. It is measure speed by Doppler velocimetry and Multiplied by the measurement time that can have the measuring length. At the same time, determines all latitude length and an average length, maximum length and minimum length. Due to limited conditions, experiment using Labview software to build the entire system testing procedures. With the operation of the system can immediately draw the critical data needed to be used. Here are the details:
Chapter 1, Introduced the steel plate and Shapemeter definition. Home and abroad the steel plate Shapemeter the research status and development trends, as well as the length of steel plate detection significance and value. According to the development status and the importance of research, design a complete set of the detection system.
Chapter 2, According to the research required to design the overall architecture of the detector system, including the positioning of sensors, Doppler velocimetry location of installation. Focus on the working principle of the length of the detection system.
Chapter 3, Make an introduction of system components and related parameters.
Focus on the working principle of the laser Doppler anemometer.
Chapter 4, Use Labview builds the block diagram and front panel, runs the virtual program to get the appropriate data, analyze the data.
Chapter 5, According to the measured data use Matlab software to write programs to analyze the data.
Chapter 6, Summary and Outlook.

Key words：Length Detection, Doppler velocimetry, The block diagram, Summing

目录
摘要
Abstract
第1章绪论 1
1.1 前言 1
1.2 课题研究现状和发展趋势 1
1.2.1 中厚板及板型仪的定义 1
1.2.2 国内外研究背景及现状 2
1.2.3 研究趋势 3
1.3 论文研究意义和主要内容 4
1.4 论文的结构安排 5
第2章中厚板板型仪长度检测系统整体框架的设计 6
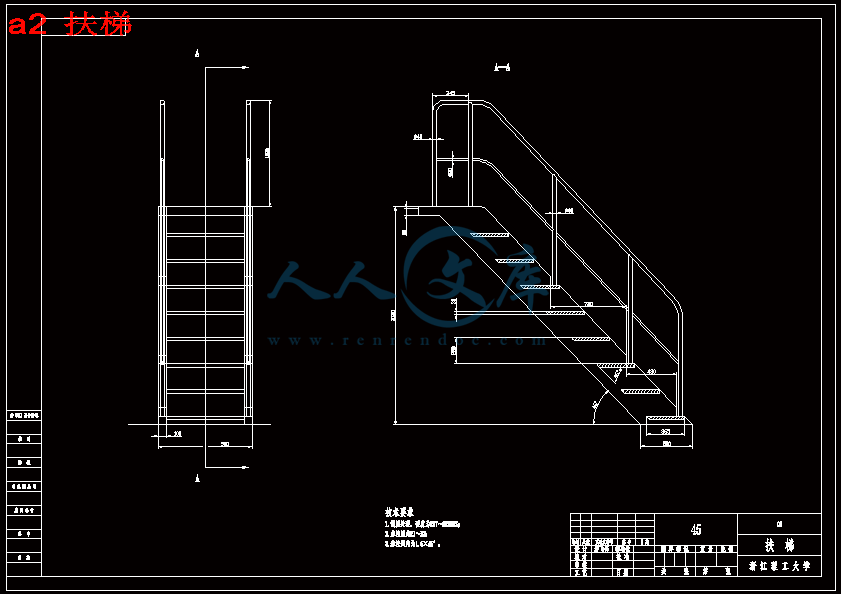
2.1 安装布局工作环境及仪器选择 6
2.2 冷轧中厚板轮廓检测仪各个子系统的功能 9
2.3 结构的受力分析 12
2.4 仪器的安装定位 16
2.5 长度检测原理和方案 17
第3章系统组成和多普勒激光测速仪 20
3.1 长度检测系统的组成 20
3.2 多普勒激光测速仪及测量原理 20
3.3 钢板长度测量过程中需要探讨的问题 23
第4章基于Labview的长度检测系统的设计 25
4.1 Labview程序图主界面的设计 25
4.2 速度测量程序框图和前面板的设计 26
4.3 长度测量程序框图和前面板的设计 27
4.4 数值显示与分析 29
4.5 小结 30
第5章 MATLAB编程 31
5.1 程序编写 31
5.2 小结 33
第6章总结与展望 34
6.1 总结 34
6.2 展望 34
参考文献 36
致谢 38
附录 1 39
附录 2 40

第1章绪论
1.1 前言
钢铁行业作为重工业和基础原材料行业，其发展状况直接影响到国民经济的稳固发展[1]。目前，我国已经成为全球最大的钢铁生产国，然而我国钢铁行业与国外相比仍存在很大的差距，其主要原因是我国钢铁行业的总体技术装备和生产集中化程度不高，因此生产的钢铁产品的品质、质量、附加值等都还远不如发达国家，导致我国钢铁产品在国际市场上缺乏竞争力[2-5]。所以如何由钢铁大国发展成为钢铁强国，其关键在于提高我国钢铁行业的生产专业化的集中程度和自动化检测技术。

内容简介：: 附件二：浙江理工大学本科毕业设计（论文）任务书寿飞锋同学（机械设计制造及其自动化专业 / 班级： 09机制4班）现下达毕业设计（论文）课题任务书，望能保质保量地认真按时完成。课题名称中厚板板形仪长度检测系统的设计主要任务与目标从发展区域看，欧洲在非接触式板形仪技术方面仍处于领先地位，如德国的LAP、Parsytec公司、英国的JONES-SHIPMAN 公司、瑞典的ASEA公司。在美国、日本和其它工业发达国家，这项技术也得到应用。早些年，我国冶金研究所，中科院曾组织这方面的研究，因现场干扰问题没有较好解决，这项技术没有推广应用。目前，我国应用于钢厂生产线上的基于激光的非接触式板形仪全部进口。基于激光的非接触式板形仪，是目前国内外最高水平的检测设备之一，主要用于钢板产线上对钢板板形的在线检测，国际上只有极少数几个工业发达国家掌握该项技术，因此该设备具有极高的研究开发价值。本课题拟以横向项目为背景，与其他同学合作开发设计中厚板板形仪。该同学在本课题中主要任务是：1）设计检测装置；2）分析中厚板板形仪长度检测原理；3）编写中厚板板形仪长度检测程序，并进行演示。目标：提出的设计方案可行，结构设计合理，完成的三维、二维图纸满足生产要求，运行程序，进行演示。主要内容与基本要求主要设计内容有：1）检测装置、传感器安装方案设计；2）与其他同学合作确定整机的设计方案； 3）检测装置、传感器安装结构设计，完成三维、二维图纸；4）编写中厚板板形仪长度检测程序。基本要求：按照课题内容，完成总体方案设计，完成三维、二维图，总计不少于2张图纸；通过编写中厚板板形仪长度检测程序，完善设计。完成毕业设计要求的各种文档，包括文献综述、开题报告、外文翻译及毕业设计论文等。严格按照进度安排，保质保量完成所承担的任务；遵守实验室规定。主要参考资料及文献阅读任务1.沈熊. 激光多普勒技术及应用M. 北京:清华大学出版社,2004 2.周坚刚,李山青,许健勇. 冷轧带钢板形自动控制概况 J .世界钢铁, 2006 3. 刘姝宇. 轧钢厂中多普勒激光测量仪的应用J. 山西冶金，2009，117：74-75.4. 陈敏，汤晓安. 虚拟仪器软件LabVIEW与数据采集J.小型微型计算机系统，2001，22(4)：501-503. 5.刘维，韩旭东，艾华. 激光三角法在位移测试中的应用.光学精密工程，206. 王香菊. 基于中值滤波与小波变换的图像去噪方法研究D.西安科技大学，2008.7.沈熊. 激光多普勒技术及应用M. 北京:清华大学出版社,2004 8.周坚刚,李山青,许健勇. 冷轧带钢板形自动控制概况 J .世界钢铁, 2006 9. Koichi Maru* and Takahiro Hata. Nonmechanical scanning laser Doppler velocimeter for cross-sectional two-dimensional velocity measurement .2012.1110. K TEORII PLASTIN SREDNEI TOLSACHINY . THEORY FOR PLATES OF MEDIUM THICKNESS 11.胡畔. 板型仪在线测量系统在四辊轧机中的应用 . 2011.8.12. 王素红.激光多普勒测速技术. 长春工业大学基础科学学院 13001213. 李文峰. 幅值谱与不变矩的特征提取方法在钢板表面检测中的应用 . 北京科技大学.200614. 徐科，孙浩，杨朝霖. 中厚板表面在线检测系统的开发与应用. 2005中国钢铁年会论文集. 中国金属学会15. 陈江宁. 现代宽厚板特殊检测仪表的应用与展望. 200116. 赵国新. 中厚板生产的发展趋势. 黑龙江冶金,2012,第2期17. 唐荻.武会宾. 我国高附加值中厚板产品现状与发展趋势. 轧钢,2012,第2期18. 王斌. 中厚板的板形检测、质量判定与优化剪切. 2011年全国中厚板生产技术交流会论文集19. 贺赛先，仲思东，王新华，何对燕. 武钢中厚板尺寸测量硬件系统. 武汉测绘科技大学学报,1996,第1-2期20.刘同波. 激光多普勒测速仪的设计及实现. 大连理工大学.200621. 张艳艳, 巩轲, 何淑芳, 霍玉晶. 激光多普勒测速技术进展. 清华大学电子工程系, 北京10008404,8.外文翻译任务阅读2篇以上（10000字符左右）的外文材料，完成2000汉字以上的英译汉翻译。英文文献参考如下：Nonmechanical scanning laser Doppler velocimeter for cross-sectional two-dimensional velocity measurementTHEORY FOR PLATES OF MEDIUM THICKNESS计划进度：起止时间内容2012.12.012012.12.30毕业设计前期资料准备、毕业设计任务书、外文翻译任务布置。2013.01.012013.01.30教师指导学生查阅资料(包括外文资料)，撰写文献综述、开题报告及完成外文资料翻译等工作。完成文献综述、开题报告及完成外文资料翻译放假前交指导教师。2013.02.012013.02.14完成文献综述、开题报告及完成外文资料翻译等等工作。指导教师审核学生上交的文献综述、开题报告及外文资料翻译等，为小组交流、开题报告答辩做准备。2013.02.232013.03.15开学第一周完成开题报告答辩工作进行总体方案设计。2013.03.162013.03.31完成检测装置、传感器安装方案设计，二维、三维图绘制；初步程序编写。2013.04.012013.04.15中厚板板形仪宽度检测分析，程序编写、调试。2013.04.152013.05.24撰写毕业论文并在教师指导下修改。2013.05.252013.05.29论文答辩实习地点指导教师签名年月日系意见系主任签名：年月日学院盖章主管院长签名：年月日3外文翻译毕业设计题目: 中厚板板形仪长度检测系统设计原文1: Nonmechanical scanning laser Doppler velocimeter译文1: 非机械破碎的扫描激光多普勒测速仪原文2: Theory for plates of medium thickness译文2: 中厚板理论0译文1非机械性激光多普勒测速仪的二维速度测量浩一丸*和孝弘羽田孜1. 绪论激光多普勒测速仪（LDV）已经被广泛地使用在许多研究和工业生产中用来来测量物体、流体的速度，因为其无创性，精细的空间的分辨率和线性响应。在光学机构中，各种用于机械扫描测定位置的技术已经成熟运用1-6。在实际应用中，具有结构紧凑，易于来处理特点的LDV传感器探头是可取的。如果打算应用常规扫描技术的一个LDV探针，那么它在探头内的使用的移动机构是必不可少的。然而，探头内的移动机构可以很容易地因为对齐或从机械冲击而损坏，探头也难以小型化。为了克服这些缺点，在常规的扫描技术的基础上，作者提出了没有任何移动的机制的探针扫描7-10。在这些LDVS中，该扫描功能是可以通过改变输入到探头的光的波长和衍射光栅扫描光束，和衍射光栅扫描光束，而不是使用移动机构都包含在探头。然而，扫描的方向被限制在一个轴向方向，即，平行于光轴的方向轴，或横向方向，在这些LDVS的光轴垂直的方向上。测量位置为流量的横截面上的一个二维扫描的液体流的速度分布的测量的在许多应用中是可取的。已报道一个LDV测量接收光学系统中使用的塑料光纤阵列的多个位置的速度11,12，虽然测量位置在一维分布并且在一个机械的阶段，却已被用于二维速度测量。在本文中，我们提出了一个非机械的，可以在二维平面上的横截面平面垂直于流动方向的扫描，没有任何移动机构在其探头的扫描LDV。结合波长的变化，以及探头的光纤阵列输入端口的变化用于执行测量位置的二维扫描。我将分别从理论和实验证明这种扫描功能。2. 原理A. 二维扫描的概念建议的非机械二维扫描LDV的概念示于图1中。如图所示， LDV包括的传感器探头包括一个衍射光栅和主体，该主体包括一可调谐激光器和光开关。在主体和探针连接的光纤阵列和电缆。从可调谐激光器的光束由光开关激发，通过光纤阵列中的纤维，然后被输入到传感器探头。在探头中，从其中一个光束光纤阵列端口进入的光束进过校直，入射到衍射光栅。当入射角度为0度时，光束对称衍射。该第一和第一级衍射光束被反射镜反射，并相互交叉在测量位置。最佳的散射光束的拍频信号来自发光二极管。信号随后被转移在主体中，信号分析器随后计算出结果。在这种结构中，可调谐激光器和衍射光栅的光开关和光纤阵列相结合用于在两个维度扫描测量位置。从测量位置沿轴向扫描，通过改变输入得到探头的光的波长。这和我们已经报道的方法相类似7。光栅的衍射角随波长变化。在测量点位置可以进行扫描。一个横向扫描功能是通过以下方式获得不断变化的的光纤阵列光开关的端口。横向测量的位置依赖于输入位置的光束探头。因此，当在横向方向上移动了光束输入的位置时，测量位置也常在在横向方向上移动。是因为可调谐激光器和光开关是可以分开的探针，探针可保持简单，可靠。图 1参考文献1 GR格兰特和KL奥尔洛夫，“双色双光束后向散射激光多普勒测速仪，”APPL。 OPT。 12，2913年至2916年（1973年）。2 ，Y. Y. T.西川，北谷，米田野，T.山田，“空间相关测量的附加喷气机通过新的扫描激光多普勒测速仪用衍射光栅，”第七次研讨会对湍流（ 1981年），第380-389页。3 B. F.德斯特，莱曼和C特罗佩亚，“激光多普勒流场快速扫描系统，”牧师科学。仪器和设备。 52，1676至1681年（1981年）。4 P.斯利拉姆，S. Hanagud，J.克雷格，NM Komerath，“扫描激光多普勒流速剖面技术检测移动表面上”; OPT。 29日，2409年至2417年（1990年）。5 EB李，AK小芹，和世界青年园“在冷轧变形区的速度分布测量的扫描LDV，”选件。激光工程。 35，41-49（2001）。6 M. Tirabassi和SJ Rothberg，“扫描LDV楔形棱镜，选件。激光工程。 47，454-460（2009）。7 K.丸“，轴向扫描激光多普勒测速仪采用波长的变化不动，在传感器探测机制，”OPT。快递19，5960-5969（2011）。8 K.丸，T.藤原，R.池内，“非机械性的横向扫描激光多普勒测速仪采用波长变化，”APPL。 OPT。 50，6121-6127（2011）。9丸和T.羽田孜，“非机械轴向扫描激光多普勒测速仪与方向的歧视，”APPL。 OPT。 51，4783-4787（2012）。10 K.丸“，非机械双轴扫描激光多普勒测速仪，”IEEE参议员，J. 12日，2648年至2652年（2012年）。11 T. Hachiga，N.古都，J.观松，K.菱田，M.熊田，“发展的多点的LDV通过使用半导体激光器的基于FFT的多信道信号的处理，用”Exp。流体24，70-76（1998）。12 ，K. D.小林，S. T. Andoh H.石田，H.白河，秋口，上山，Y.仓石，T. Hachiga，“微血管三维成像技术使用的多点激光多普勒测速仪“，J.;物理。 106，054701（2009）。13 JE哈维和的CL Vernold“的方向余弦空间衍射光栅的行为的描述，”APPL。 OPT。 37，8158-8160（1998）。14 M. Pascolini，S. Bonora，A. Giglia，N. Mahne，S. Nannarone，L. Poletto，“在一个圆锥形的衍射光栅安装一个极端的紫外线时间延迟补偿单色”; OPT。 45，3253-3262（2006）。15 H.-E.阿尔布雷希特鲍里斯，N.达马施克，和C.特罗佩亚，激光多普勒和相位多普勒测量技术（施普林格，2003年），第7.2节。16 ，Y.，Y.泷田华启青木，A. Sugama，S.青木，H.奥纳卡，“44光突发交换使用PLZT光束偏转器的高速交换子系统与VOA（10微秒） “在光纤通讯研讨会及展览会和全国光纤工程师会议，技术精华（CD）（美国光学学会，2006年），纸OFJ7。17 IM Soganci，T.种村，KA威廉姆斯，N. Calabretta，T. de Vries先生，E. Smalbrugge，MK斯密特，HJS Dorren和华野，“高速16的InP单片集成光开关，”诉讼2009年第35届欧洲光通信会议（ECOC 09）（IEEE 2009），本文1.2.1。18 K.梨本，D. Kudzuma，H.汉，“高速开关和过滤使用PLZT波导器件，”在15日光电子和通信会议（OECC 2010）（IEEE 2010），纸8E1-1的诉讼。19 SH云，C. Boudoux，GJ Tearney，鲍马，的“掠高速波长的半导体激光与一个polygonscanner basedwavelength过滤器，”选项。快报。 28，1981-1983（2003）。20 ，H. K.加藤，R. N.藤原吉村，石井，F.卡诺，Y.川口，Y.近藤，K. Ohbayashi，并H. Oohashi，“140 nm的准连续快速扫描使用SSG-DBR激光器，“IEEE光子。技术快报。 20，1015-1017（2008）。原文2THEORY FOR PLATES OF MEDIUM THICKNESS(K TEORII PLASTIN SREDNEI TOLSACHINY)A theory of elastic isotropic plates of constant thickness is constructed without assumptions about the nature of the deformations of the transverse linear elements.The stresses xx, xy, yy are expanded in a series of Legendre polynomials Pk (2z/h). The remaining stresses are found from equilibrium equations after application of Castiglianos principle.The expansion of unknown quantities in Legendre polynomials was applied to the shell theory by Cicala I. But he made use of the principle of virtual displacements, which does not reveal all the advantages of these series over power series.Application of the Castigliano principle gives the possibility of using these advantages effectively with the result that expansion in Legendre polynomials permits a separation of those parts of the stress for which the principal vector and moment is equal to zero. Because of this circumstance the boundary condition is formulated in the most convenient form for application of the St. Venant principle.By neglect of terms of the order of (h/a)* by comparison with unity (h, plate thickness, a, plate width) one may obtain the equations of classical plate theory from those of the present theory. Conservation of these terms leads to exact equations which contain other terms besides those in 2-41.1. The middle surface of the plate is described by a Cartesian rectangular xyz coordinate system. Besides the xyz coordinates we introduce the nondimensional coordinatesThe stresses xx, xy, yy in the plate are represented in the form of Legendre polynomials in the coordinate Here and from now on the symbol (xy) signifies that analogous relations for other quantities are obtained by the interchange of x and y. By virtue of the orthogonality of the Legendre polynomials, Txx, . . . .Myy have the significance of forces and moments, and Pk() kxx . . . . self-equilibrating stresses through the plate thickness.For simplicity we consider the surfaces z = h/z of the plate to be loaded by only continuously distributed normal loadsSubstitution of the Expressions (1.1) into the equilibrium equations of the theory of elasticity and integration with respect to z using (1.2) gives expressions for the remaining stress components (mass forces omitted)and the equilibrium equations for forces and momentsThe quantities Vx and Vy represent shear forces and Akx, Aky determine self-equilibrating shear forces through the thickness.It follows that Expressions (1.1) and (1.3) satisfy the equilibrium equations of the theory of elasticity and the boundary conditions (1.2), if forces and moments are introduced therein satisfying the equilibrium equations (1.4) of plate theory.For determination of the quantities Txx，Mxx ，kxx. we make use of the Castigliano principle; the problem leads to an extremum condition since the forces and moments must be subject to Equations (1.4).As usual, we use the method of Lagrangean undetermined multipliers. We insert the left-hand sides of Equations (1.4) inside the integral for potential energy of the plate, multiplying each by an undetermined multiplier. As a result we obtain the functionalHere u, v, , x ,y are Lagrangean multipliers. The double integral is taken in the middle surface of the plate.Formulas (1.1) and (1.3) for stresses are inserted into (1.6) and the variation of the functional is equated to zero. The variational equation will result in relations which must be satisfied in the middle surface of the plate.If only the first four terms are retained in the series (1.1) (kxx =kxy =kyy = 0, k4), these equations take the following formIn addition, on the contour of the regionmust hold.The quantities under the integral sign are components corresponding to vectors and tensors, referred to the external normal n and the tangent s of the contour. Quantities in the square brackets will not be used and we shall not discuss them. The static and geometric (homogeneous) boundary conditions follow from Equation (1.12).Note that if only the first two terms in series (1.1) are retained, the plate theory of Reissner 4 is obtained. If, in addition, the stresses xx, xy, yy are neglected in the functional (1.6 ) the plate theory of Kirchoff is obtained.By consideration of the obtained equations it is easy to find that the problem of stress determination splits into two independent problems. The first problem consists in solving equations of the type of (1.7), (1.8) and the first of (1.4) with corresponding boundary conditions from (1.12), The second problem consists in solving equations of the type of (1.9), (l.l0), (l .l l), and the second equation of (1.4) with the corresponding boundary conditions.In the future we shall limit ourselves to the case where only the first four terms are retained in the series (1.1); (b = 2, 3).From the obtained system of equations one may derive another system for the determination of the self-equilibrating stresses, kxx, kxy, kyy through the thickness of the plate (excluding forces, moments and displacements appearing as Lagrangean multipliers). The coefficients for the derivatives of different series are small numbers, the smaller the higher ;he order of the derivative. In view of this, a more general solution for such a homogeneous system will be expressed by a rapidly varying function, and a particular solution is easily calculated with sufficient accuracy. It will also be determined during a study of the state of stress in the plate remote from the edge as a rapidly varying .part of the solution by virtue of the St. Venant principle (since knn,kns ,Akn at the edge of the plate determine stresses, self-equilibrating through the thickness) localized at the edge of the plate and decaying rapidly away from it.In this work on stress determination we have limited ourselves to consideration of a particular solution of the above equations not giving the state of stress localized at the edge of the plate. For this, terms of the order of (h/a)2 must be retained n the formulas or the stresses xx, xy, yy and terms of the order of (h/a)4 neglected by comparison with unity.2. We consider the second problem. The shear forces and moments arising from the action of the surface forces (1.2) have the following orders(assuming that the external loads are such that the order of the quantities considered does not reduce upon differentiation with respect to .).The particular solution of Equation (1.10) with an accuracy to terms of the order of (h/a)2 has the following form:We conclude from these equations, as well as from.(2.1) and (1.5), that the bracketed terms in (1.9) are as small by comparison with the left-hand side of (1.9) as (h/n)4 is by comparison with unity, and these terms must accordingly be rejected in the simplified system.The expressions obtained for momentsCoincide with the formulas of Reissner 4 and Armbartsumian 2. These formulas would be obtained if the last term on the right in (1.11) were neglected. Therefore one must takeThe formulation of the edge problem coincides with the edge problem in the work of Reissner 4, but differs from the edge problem in the work of Ambartsumian 2. Thus, in the work of Reissner the edge condition is equivalent toand in the work of Ambartsumian toCondition (2.5) is obtained by a variational method. The left-hand side has the significance of a generalized displacement, in which work of the moment Mnn is done. The left-hand side of (2.6) has no such significance. Therefore the edge condition (2.6) does not answer the requirement that the reaction of the support do no work, and it must be regarded as inconsistent. The result of this will be a nonselfconjugate edge problem. Thus, the edge problem in the present formulation agrees with the edge condition for plate bending of Reissner. The difference consists in the formulas from which stresses are calculated after finding the forces, moments and displacement w. Thus the stresses xx, xy, yy are determined from the formulasin accordance with (l. l), (2.2) and (2.3). The first terms on the right-hand side give stresses as calculated from the classical theory of plates. The remaining terms give the corrections of the order of (h/a)* compared with unity. If terms P5 ()5xx , P5() 5xy, P5() 5xz, were retained in the series (l . l), then the corrections obtained would be of a still higher order than (h/a)2. In the Reissner plate theory the stresses areA comparison of Formulas (2.8) to (2.10) with those of (2.7) shows that certain terms are missing from the less exact formulas, terms having in general the same order as those already retained. The reason for this is that Reissner starts with a linear distribution of the stresses. xx, xy, yy through the thickness; other authors 2,3 introduced other simpifying assumptions with an unknown error in the determination of stresses and displacements.3. We return to the problem of the momentless deformation of a plate. We assume that the stresses induced by forces applied at the edge of the plate all have the same order as the bending stresses (i.e. p(a/h)2); let q pThe particular solution of Equation (1.8) with accuracy to terms in (h/a)2 compared with unity will be Considering that Txx， Tyy = ph(a/h)2 and referring to (1.5), we conclude that the bracketed terms in (1.7) are as small in comparison with the left-hand part of (1.7) as (h/al4 is compared with unity, and accordingly those terms must be omitted in the simplified system. We obtain These formulas are also found in 2, 3in which they determine the membrane stresses. In the present work .the stresses are given by the formulasin agreement with (3.1) and (1.1).If the terms P4()4xx , P4() 4xy, P4() 4yy, are retained in the series (1.11, then the corrections obtained will be of a higher order of smallness than (h/a)2 as compared to unity.BIBLIOGRAPHY1.Cicala, Placido, Sulla teoria della parete sotile. Giorn. Genio ciuile 97, NOS. 4, 6, 9, 1959.2.Ambartsumian, S. A. , T

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。