人人文库网 > 图纸下载 > 毕业设计 > 液压挖掘机正铲工作装置设计【优秀含4张CAD图纸+proe三维建模及仿真+挖掘机机械全套课程毕业设计】

论文.doc

液压挖掘机正铲工作装置设计【优秀含4张CAD图纸+proe三维建模及仿真+挖掘机机械全套课程毕业设计】

资源目录

液压挖掘机正铲工作装置设计【优秀含4张CAD图纸+proe三维建模及仿真+挖掘机机械全套课程毕业设计】.rar

论文.doc---(点击预览)

摘要.docx---(点击预览)

开题报告.doc---(点击预览)

学士学位论文原创性声明.doc---(点击预览)

外文翻译.doc---(点击预览)

lunwen封面目录.docx---(点击预览)

A model of the working operatiors__ of a quarry excavator.pdf---(点击预览)

proe三维建模

chandougang1_3.prt.1

chandougang222.prt.2

chandougang2_2.prt.2

chandou_31.prt.2

dongbigang2_1.prt.3

dougangang1_2.prt.3

dougangang2_2.prt.2

dougan_53.prt.2

prt0001_53.prt.2

suan08_1.prt.1

suan09_1.prt.1

suan1_2.prt.1

suan2_2.prt.1

suan3_2.prt.1

suan4_1.prt.1

suan5_1.prt.1

suan6_1.prt.1

suan7_1.prt.1

wajuejijiti_10.prt.3

zpt1_asm_14.asm.1

zpt1_new.asm.8

动臂.dwg

动臂、斗杆长度.dwg

工作尺寸.dwg

斗杆.dwg

油缸参数.dwg

液压正铲挖掘机机构简图.dwg

装配图.dwg

转角范围.dwg

运动仿真.mpg

铲斗.dwg

压缩包内文档预览：(预览前20页/共35页)

编号：449326 类型：共享资源大小：5MB 格式：RAR 上传时间：2015-07-05 上传人：QQ14****9609 IP属地：陕西

50
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: 液压挖掘机工作装置机械设计机械毕业设计液压挖掘机正铲工作装置设计 proe三维建模及仿真挖掘机机械全套课程毕业设计

资源描述：

液压挖掘机正铲工作装置设计【优秀含4张CAD图纸+proe三维建模及仿真+挖掘机机械全套课程毕业设计】

【带开题报告+外文翻译】【39页@正文13600字】【详情如下】【需要咨询购买全套设计请加QQ1459919609 】

A model of the working operatiors__ of a quarry excavator.pdf

lunwen封面目录.docx

外文翻译.doc

学士学位论文原创性声明.doc

开题报告.doc

摘要.docx

论文.doc

proe三维建模

动臂.dwg

动臂、斗杆长度.dwg

工作尺寸.dwg

斗杆.dwg

油缸参数.dwg

液压正铲挖掘机机构简图.dwg

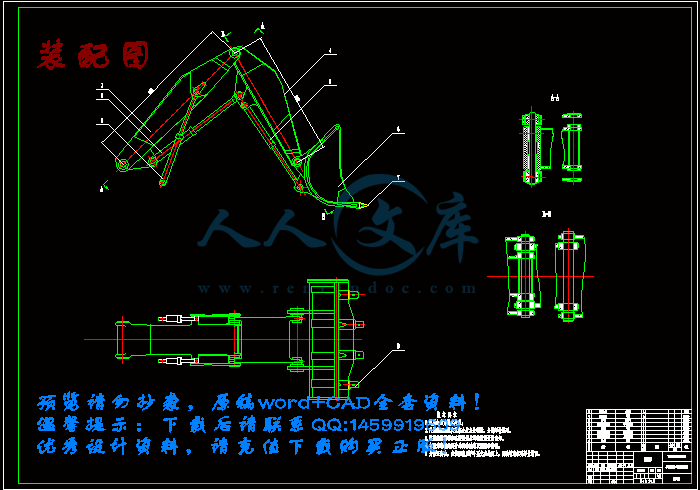
装配图.dwg

设计文档

转角范围.dwg

运动仿真.mpg

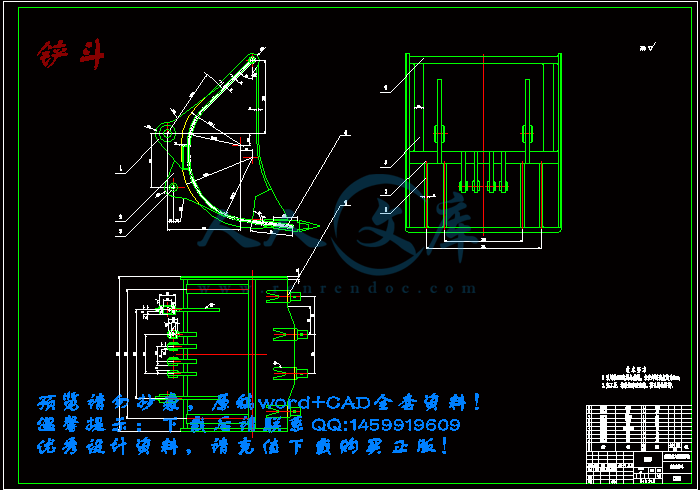
铲斗.dwg

液压挖掘机的的发展及设计

摘要：近年来，随着钢铁业、煤炭业、电力业的持续迅猛发展，挖掘机等工程机械的需求日益增加，并广泛地运用于房屋建筑、筑路工程、水利建设、农林开发、港口建设、国防工事的土石方施工和矿山采掘工业中。由于其作业工况复杂多变，挖掘方式往往是凭借操作者的经验，根据实际作业工况决定，为了减小操作者的挖掘经验对挖掘效果的影响，就迫切需要建立起铲斗挖掘轨迹与各液压缸的直接对应关系，实现挖掘机操作的自动化。同时由于挖掘机的工作环境的复杂性及工况的多变性，就要求液压挖掘机本身结构要根据环境的不同作相应的调整，这就决定了挖掘机设计的平凡性、重复性。然而液压挖掘机的工作装置又是一个多自由度的多杆系统，各铰点的确定非常复杂，这些因素就造成了液压挖掘机的投资大、设计周期长，严重地影响了厂商的经济效益及国民经济的发展。

本文主要的设计工作主要有以下几个方面：在现场测绘及参考有关资料的基础上了解液压挖掘机的工作方式及工作环境。确定液压挖掘机各个工作装置的结构，查找相关资料并结合经验公式对挖掘机工作装置的总体进行设计，用比例法和经验公式计算出工作装置各部分的基本尺寸并对其进行应力分析，然后绘制出其二维CAD图纸，继而用PRO/E画出各装置的三维模型。将各装置装配后对其进行运动模拟仿真。

关键词：挖掘机；工作装置；CAD;PRO/E;运动仿真

The development and design of hydraulic excavator

Abstract：In recent years, as steel, coal industry and quarrying continued rapid development, excavators engineering machinery requirement increasingly, and is widely used in housing construction, road engineering, water conservancy construction, forestry development, port construction, national defense construction and conditions of fortifications mining extraction industryDue to the complex and changeable, mining operation condition is often with operator way according to the actual working experience, decision, in order to reduce homework to excavate the mining experience operator, the effects will is in urgent need to build up the bucket with various hydraulic cylinder dig trajectory direct corresponding relation, realize the automation. Excavator operationAt the same time because of the complexity of an excavator working environment and conditions, requires the fluidity of hydraulic excavator itself according to the different structural environment makes the corresponding adjustment, this determines the excavator design of ordinary sex, repeatability. However hydraulic excavator working device is a much more freedom, the hinge point bar system to determine the very complex, these factors will cause the hydraulic excavator big investment, design cycle is long, the serious influence on the economic benefits of the manufacturers and national economic development.

This paper mainly design work mainly in the following aspects: in the field surveying and mapping and reference on the basis of relevant information about the hydraulic excavator way of working and working environment Determine the hydraulic excavator, each working device search relevant material and structure of practical experience formula of the overall work device for excavators designed, use proportion method and experience calculation work device each part of basic size and carries on the stress analysis, and then plot its two-dimensional CAD drawings, and then painted with PRO/E 3d model of each device. After each device assembly of its motion simulation

Keywords: Hydraulic Excavator; Working device; Boom;Stick;Face-shovel

1 前言1

1.1课题研究的背景和意义1

1.2 液压挖掘机研究现状及发展动态1

1.2.1 国外的研究现状及发展动态2

1.2.2 国内的研究现状及发展动态3

1.3 本文研究的主要内容4

2液压正铲挖掘机工作装置的运动分析5

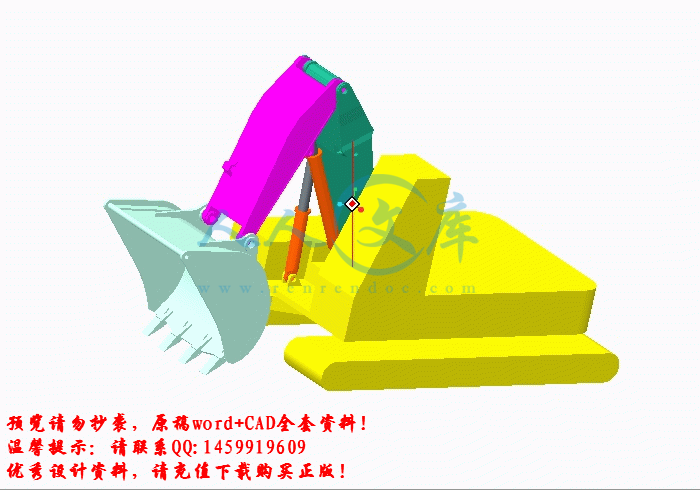
2.1 液压正铲挖掘机的基本组成和工作原理5

2.2 工作装置结构方案的确定6

2.3 工作装置运动分析9

2.3.1动臂运动分析9

2.3.2斗杆运动分析11

2.3.3斗齿尖的几种特殊工作位置的计算12

3 工作装置尺寸的设计确定15

3.1应用举例15

3.1.2动臂及斗杆长度确定16

3.1.2机构转角范围确定17

3.2 油缸铰点及行程确定17

3.2.1动臂油缸的铰点及行程确定17

3.2.2 斗杆油缸铰点及行程确定17

3.2.3 铲斗油缸铰点及行程确定18

3.3工作装置的位置模型建立18

3.3.1 动臂与平台铰点位置C的确定18

3.3.2 动臂及斗杆长度的确定19

3.3.3 机构转角范围确定19

3.4工作装置油缸铰点及行程确定24

3.4.1动臂油缸的铰点及行程确定24

3.4.2斗杆油缸铰点及行程确定27

3.4.3铲斗油缸铰点及行程确定30

3.5液压正铲挖掘机三维模型32

4 结论33

参考文献34

致谢35

1 引言

1.1课题研究的背景和意义

目前我国露天矿的开采规模逐渐扩大，为了适应日益增大的矿用汽车铲装的需要，这就需要较大斗容的挖掘机，由于挖掘机愈大，每单位土石方的施工成本愈低，而液压挖掘机较机械式挖掘机有很多优点，但是国内对大型液压正铲挖掘机的研究较少，液压挖掘机工作装置是完成挖掘机各项功能的主要构件，其结构的合理性直接影响到挖掘机的工作性能和可靠性，对其研究是整机开发的基础，对工作装置进行优化，目的在于缩短研究和开发周期，降低产品成本，提高设计质量，本课题的任务就在于此[1]。

现代化建设速度，在很大程度上取决于各种工程建设速度，而工程机械水平的高低，又直接对工程建设速度发挥着促进或抑制作用。传统研发管理及设计方法只是被动地重复分析产品的性能，而不是主动地设计产品的参数。作为一项设计，不仅要求方案可行、合理，而且应该是某些指标达到最优的理想方案。随着电子计算机的应用，在机械设计领域内，已经可以用现代化的设计方法和手段进行设计，来满足对机械产品提出的要求。利用优化设计方法，人们就可以从众多的设计方案中寻找出最佳设计方案，从而大大提高设计效率和质量。可靠性是我国工程机械的致命弱点，我们要正视差距，增强科研开发力度，提高技术水平，更多地发展具有自主知识产权的高质量产品，进一步促进工程机械的发展[1]。

参考文献

1．王新中.国内外矿用挖掘机发展状况[J].矿山机械，2004(9):52-53

2．矿用挖掘机发展方向[J].中国矿业报,2002,16(7):255

3．张宏，赵光.从慕尼黑 bauma 展看当今挖掘机技术发展[J]，建筑机械化，2007,6:8-10

4．张润利，刘伯颖.工程机械专利信息之小型挖掘机篇[J]，工程机械，2006(4):21-26

5．方良周.MX80 液压挖掘机工作装置的仿真与铲斗机构的优化[D].沈阳：东北大学，1996

6．同济大学等.单斗液压挖掘机(第二版)[M].北京:中国建筑工业出版社，1986,12:50-114

7．赵培训.单半液压挖掘机工作机构运动分析参数优化和动态模拟系统的研究[D].西安：西安公路交通大学，1998

8．范进桢，孟宪慧等.挖掘机挖掘作业工程的动力学研究[J].矿山机械，2005，09：39～41

9．史清录，林慕义，康健.挖掘机的最不稳定姿态研究.农业机械学报[J]，2004(9): 32～35

10．张石强.正铲液压挖掘机挖掘性能通用分析方法研究[D].重庆：重庆大学硕士学位论文，2006,10

11．冯培恩，陈文平，潘双夏.复杂机械CAD系统开发策略及应用实例[J].机械工程.1989 (4): 6-9

12．潘双夏，冯培恩，郭建瑞，全永新.液压挖掘机智能CAD策略研究.机械工程[J]， 1991(10):19-22

13．曹善华.单斗挖掘机[M].北京：机械工业出版社，1988:1-102

14．唐银启主编.工程机械液压与液力技术[M].北京：人民交通出版社，2003,5:85-86

15．（日）村冈虎雄著，李宗国译.油缸[M].北京：机械工业出版社，1974,9:69-72

16．赵应樾.常用液压缸与其修理[M].上海：上海交通大学出版社，1996,2:12-15

17．Serwach Andrzej; Frydlinski Stefan;Jabikowski, etc. Parametric Optimization of the Hydraulic System of the Excavator [J]. Staub-Reinhaltung der Luft, 1974,(30):26-31

19．BRACH I.Hydraulic excavator systematic study of jib/lift cylinder connections.Foerdern Heben.1971, 21(5):56-60

20．Ward Peter, Wakeling Andrew;Weeks Richard,etc.Design Of An Excavator Arm Using Optimization Techniques [J].SAE Technical Paper Series, 1987,(5):64-67

铲斗.gif

动臂.gif

装配图.gif

内容简介：: MECHANIZATION AND AUTOMATION OF MINING OPERATIONS A MODEL OF THE WORKING OPERATIONS OF A QUARRY EXCAVATOR E. V. Gaisler, A. P. Mattis, E. A. Mochalov, and S. V. Shishaev We develop a methematical model of the process of open-pit mining with a quarry ex- cavator using a bucket that has active blades driven by impact blocks installed in the front wall. The bucket operates as follows. When the bucket comes in contact with a rock area that can be broken by a force greater than the sum of the forces of friction of the tool on the sleeve and the force of activation of the starting device, the impact blocks are energized. The action of these blocks causes the bucket blades to enter the rock to a depth X, weakening the zone located directly under the blades and forming the so-called disrupted bonding zone i. This zone requires much less force to be broken than an in- tact mass. With such active buckets, strong rocks can be excavated without preloosening. The main parameters describing the movements of the bucket during excavation include the mechanical properties of the rock, the variation of these properties under the effect of the impact, the working characteristics of the drives of the actuator mechanisms, and the parameters of the equipment. Two types of destruction take place during the course of excavation: cutting and impact breaking. The geometric sum of forces acting on all the faces of a blade represents the resist- ance to intrusion. The projection of this sum onto the axis of the impact block is Pl; the projection onto the direction perpendicular to the axis is P2. The sum of forces act- ing perpendicularly to the bucket-traveling plane is equal to zero because block fracturing is mainly performed. The following assumptions are made for a mathematical model describing the motions of the bucket: ? - the center of mass of the rock in the bucket is stationary relative to the bucket; - chips are separated continuously; - the loads on the bucket blades are equal; - the blades penetrate the rock instantaneously upon impact; -the resistance to the bucket-filling is disregarded; - the moment of friction relative to the rotation axis of the arm is disregarded. With these assumptions, the motion of the bucket can be interpreted as the motion of a two-dimensional mechanism under the effect of external forces, which includes the force developed by the drives of the pressure mechanism and the lift mechanism, the gravity force, and the resistance force of the rock face. The position of the bucket at each point in time is defined by the coordinate r(t), the distance (OC), and (t) - the angle between the boom and the bucket stick. The kinetic energy of this mechanism is expressed as = ( + m) ,- + JT (1) where m 1 is the rock mass and the bucket; m 2 is the mass of the stick and the empty bucket; J is the moment of inertia of the bucket with rock and the stick relative to its rotation axis Institute of Mining, Siberian Branch, Academy of Sciences of the USSR, Novosibirsk. Trans- lated from Fiziko-Tekhnicheskie Problemy Razrabotki Po!eznykh Iskopaemykh, No. 2, pp. 60-67, March-April, 1991. Original article .submitted September 25, 1990. 0038-5581/91/2702-0131512.50 9 1992 Plenum Publishing Corporation 131 ntsY = ml (r + lCBii)+ J + mi(r- rl) 2 + IGA), (2) where J1 is the moment of inertia of an empty bucket and the stick relative to the center of mass and r - rl is the coordinate of the center of mass of the empty bucket with the stick. The rock mass in the bucket m depends on the path traveled by the front edge of the bucket and the initial shape of the rock face. In order to write an expression for the rate of mass increment, we will consider the scheme in Fig. 2. Suppose that the path traveled by the bucket edge by the time t is described by the curve f2(r2, 2) The ini- tial shape of the face by the curve f3(r3, 3), where r2, , r3, 3 are polar coordinates with the origin at zero. During the time dt the bucket edge travels a distance ICDI; in that case, since d 2 = d 3 the mass increment within the time dt is specified by I dm = T ,B (I OC l I OD I -I OA . I OB I) sin da 2, where 0 is the rock density and B is the width of the bucket edge. We see from the diagram that loci = r, ION = r= dr, IOAI = r, IOBI = r dr3. Considering that sinda da 2 and disregarding the squares of the infinitesimal variables, we write 1 a, = r,z (, - d) a. The increment d 2 is equal to the product at the angular speed of the stick at the time t and the increment dt, i.e., d 2 = da 3 = &dt. The rate of increment of the mass is now ex- pressed as dNl o , = .-7- = _ ,i (d - ,.:,) =. (3) The mass falling into the bucket during the time t is defined by ! m, = J s ()dT 0 This mass m I is only a function of the time t. Making use of the fundamental equation of the dynamics of a variable-mass point (Mesh- cherskiis equation), we can demonstrate that Lagrangian equations are applicable to the mechanical system that consists of variable-mass material points if the absolute velocity of the associated mass is equal to zero. Consider a mechanical system comprised of n material points with masses ml, m 2 . m i, ., m n, that move with velocities v i. Lagrangian equations for m i = const have been derived in 2, p. 340. Consider the case of m i = mi(t). In following 2, we introduce generalized coordinates q, such that i = ri(ql, q2, , qs, t), where r i is the position vector of the ith mass. Now, i = )1 )j, Oli Oi j I uqj Uqj Oq) where j is generalized velocity. The kinetic energy of the mechanical system at any time point is defined as 1 - T ?niViU i . We find partial derivatives of kinetic energy with respect to the generalized coordinate qj and the generalized velocity j: or = - oi aqj miUi -r- , i=l aqi 132 nts_ ih, i - Or i OT mivl mivi Oqj = i=1 Oqj i= Oqj We differentiate this expression with respect to time . Consider now the first sum, taking into account the fundamental equation of the dynamics of variable-mass point for the case where the absolute velocity of the associated mass is equal to zero 2, p. 143 , am v =F, m.-7 + - where P is the resultant of the forces applied to the point. For a nonfree material point with variable mass, we have elT, i dm - m l -77 + -d-f vi = F., + 7 , where Ri is the resultant of the reactions of constraints applied to the ith point. Now, 7, + m, - . , + 7, + 7, - , = i=1 S - - . Or i = (F+n)=Q+&. i=l The second sum is, in fact, 8T/Sqj 2, p. 342. We obtain dt = Qj + o + OT Oq) For a system with stationary perfect constraints QjR = 0 d OT 07 It is the Lagrangian equation for a mechanical system consisting of variable-mass material points under the assumption that the absolute velocity of the associated mass is equal to zero. As we see, it is identical to a Lagrangian equation derived for a constant mass of material points belonging to the mechanical system. The Lagrangian motion equations for this mechanism are r - u-7- = QJ 7 , ,A , - = Q (5) where QI, Q2 are generalized forces acting on displacements 6r and 6, respectively, l Q, = - , o, ( - /- ,-o., / o - + :,- ,.o I + + (m + m).gcos(- ), O, = l).r.sin(-OCD) r + I CDI/ ) .P.sin cos (n - OCD) / (6) 133 ntsFig. 1 Fig. i. Fig. 2. C D Fig. 2 Design scheme for an excavator with an active bucket. Evaluation of the increment of rock weight in the bucket. 12(t). t + P3, (10) where U is the coefficient of friction of the tool in the bucket sleeve Pa as the force of activation of the automatic starting device. The stroke is made at the time l= 11+ Tl+ T2, where T l is the actuation time of the device and T 2 is the impact cycle time. Upon impact, blades penetrate the rock to a length which is a function of the rock properties, the blade geometry, and the impact energy. Studies in situ and laboratory experiments measuring the penetration of the blade upon impact, conducted by the Institute of Mining, the iInstitute of Construction Machines, the Skochinski Institute, and the Karaganda Polytechnic 4-6, suggest the existence of some characteristic of the bed being fractured which can be used to assess the fracturing efficacy. For such a characteristic the specific energ 7 capacity of fracturing can be used and measured per a unit of strength of the bed, e.g., the rocks ultimate uniaxial compressive strength, i.e., i A.K E, = .,./,.% 2.78t(I -, (11) where A is the single-impact energy, J; K 0 is the transfer coefficient of the impact energy to the bed; x is the penetration of the blade in one stroke, m; F is the transverse cross sectional area of the fracturing track m2; and o 0 is the ultimate uniaxial compressive strength of the rock, kN/m 2. The value of E 0 depends on the mechanical properties of the bed and its condition. The range of specific destructive energy capacity per stroke in certain permafrost grounds with a tool shaped as a symmetric wedge, measured by a single stroke of the density gauge devised by the Road Construction Research Institute, is indicated in Table i. The pene- tration of a blade can be defined by A.K.2.78.10-7 E,I 9 I:. % :33.3 Besides, E 0 can be measured experimentally or estimated from the data reported in 7-9. After the impact, the movement of the bucket is described again by Eqs. (2) and (8), but with the condition P = 0, P2 = 0, until the front edge of the bucket travels the dis- tance x. 135 ntsg, deg 4 5 , sec Fig. 3. Bucket stick rotation angle vs. time (i - digging without adjust- ment for C weakening after impact, 2, 3 - linear and quadratic weakening of C, respectively; 4 - experimental data; i-3 - rock (f = 5; C l = 30 x 106 H/m2; = 0.5), 4 - siltstone f = 5-6, C I = (32-36)106 N/m2; = 0.5. The condition for transition to mode 3 in time appears as 2 2 1 2 (t) + r2 (l) - 2 .r, (4).r (/:). cos ( (l) - (t) x . ( 12 ) After (12) is satisfied, cutting in mode 3 begins. The rock resistance to destruction is generally described by the familiar expression = o.tgp+ C, (13) where o is normal pressure, 0 is the internal friction angle, and C is the rock cohesion. The Mohr-Coulomb criterion can be formulated as a function of principal stresses under destructive load i0: o, = o0+ 03 9 tg2(5 + p/2), (14) where o I is the largest principal stress corresponding to the maximum of the stress-strain curve. Expressing o I and o 2 in terms of T and o and solving simultaneously Eqs. (13) and (14), we obtain an expression of the uniaxial compressive ultimate strength o 0 as a function of cohesion C: Oo= 2 .C .tg(45+ 0/2). Expression (15) shows that the main characteristic of the alteration of rock properties after impact is a drop in cohesion. The cohesion in the bed is defined as (15) C = C,l, (16) where C I is rock cohesion in a lump; 11 is the structural weakening coefficient of the bed, which is a function of the average lump size, the main crack network, and the direction of the mine advance 8. After the impact, the cohesion C(t3) = C.2, where 12 is a coefficient representing additional weakening of the bed by impact loads. At the load application point, the material is crushed. According to Popov 7, k2 after the impact is reduced to 0.0005. As the blade moves through the disrupted bonding zone, the value rises to its initial level according to a certain pattern (studying the behavior of C = f(x) is a separate subject). In a first approximation, the size of the zone and the cohesion value can be estimated from the results of 7-9. The movement of the bucket in the disrupted bonding zone is described by (2)-(10), plus additional con- straints imposed on C (the rock cohesion). With increasing C, the values of Pl and P2 grow. The further movement of the bucket follows mode 1 or 2, depending on whether con- dition (i0) is met. 136 ntsEquations (2)-(8) hold for all the modes of bucket movement, with the respective con- straints imposed on P1, P2, and C. Transitions between the modes occur depending on whether conditions (9) and (i0) are satisfied. A mathematical model composed of (4), (6), and (8), which describes the working process of an excavator with an active bucket, consists of a set of nonlinear differential equations. A modified Merson algorithm with an automatic step selection and accuracy control was used to solve this sytem. The model has been programmed for a computer in an interactive mode. In the course of solution, the trajectory of the bucket can be adjusted by selecting load characteristics of the drives of lift and pressure mechanisms, i.e., by choosing the appropriate functions fl(), f2(, &), which correspond to the actual process of excavator control. Several alternatives were computed to evaluate this model. The results are illustrated by solid plots in Fig. 3. In the first situation, the fracturing is caused entirely by impact loads. The energy of a single stroke is insufficient to create a disrupted bonding zone (curve i). The other two cases are characterized by different forms of weakening of cohesion in the dis- rupted bonding zone (2, linear weakening; 3, quadratic weakening). The modeling results were compared with the data of in situ experiments on siltstone in the Krasnogorsk section of Kemerovougol Enterprises (dashed line in Fig. 3). A qualitative similarity was observed between the model and the actual process (the data discrepancy did not exceed 30%). The smallest discrepancy was observed with the linear cohesion weakening in the disrupted bond zone. With his mathematical model one can investigate the parameters of the working process in various !excavation conditions for design of these machines to meet specific technical and economic characteristics and mining objectives. LITERATURE CITED i. A. I. Fedulov and V. N. Labutin, Impact Coal Destruction in Russianl, Nauka, Novo- sibirsk (197

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。