人人文库网 > 图纸下载 > 毕业设计 > 简摆腭式破碎机设计【8张CAD图纸和说明书】

设计说明书论文.doc

简摆腭式破碎机设计【8张CAD图纸和说明书】

资源目录

简摆腭式破碎机设计【8张CAD图纸和说明书】.zip

外文翻译

A0-装配图.dwg

A1-动腭.dwg

A2-地基图.dwg

A2-大带轮.dwg

A2-曲轴.dwg

A2-连杆.dwg

A2-连杆体.dwg

A3-小带轮.dwg

压缩包内文档预览：(预览前20页/共53页)

编号：6039297 类型：共享资源大小：2.08MB 格式：ZIP 上传时间：2017-10-26 上传人：俊****计 IP属地：江苏

40
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: 破碎机设计 8张 cad 图纸说明书

资源描述：

1 概述

2 物料破碎及其意义

2．1 物料破碎及其意义 3

2．2 破碎物料的性能及破碎比 5

3 工作原理和构造

3.1 工作原理 10

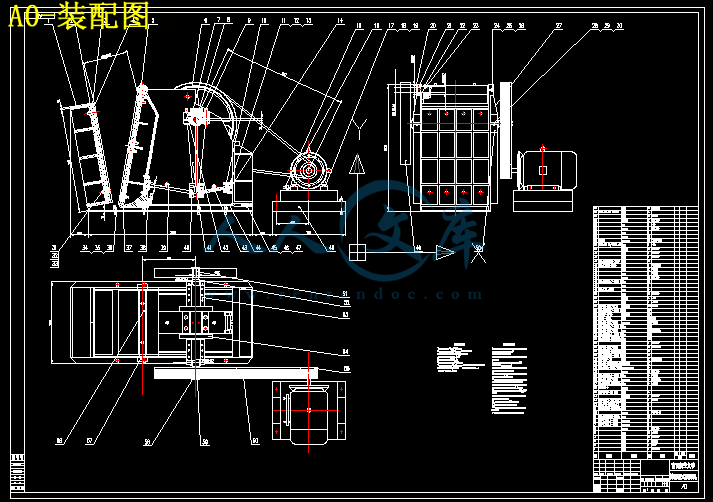
3.2简摆腭式破碎机的结构 11

4 主要零部件的结构分析

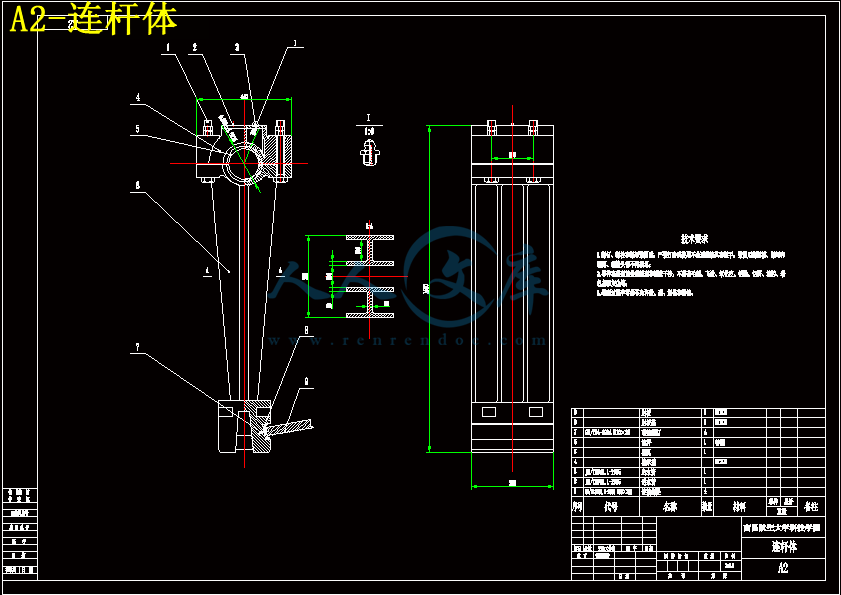
4.1连杆 14

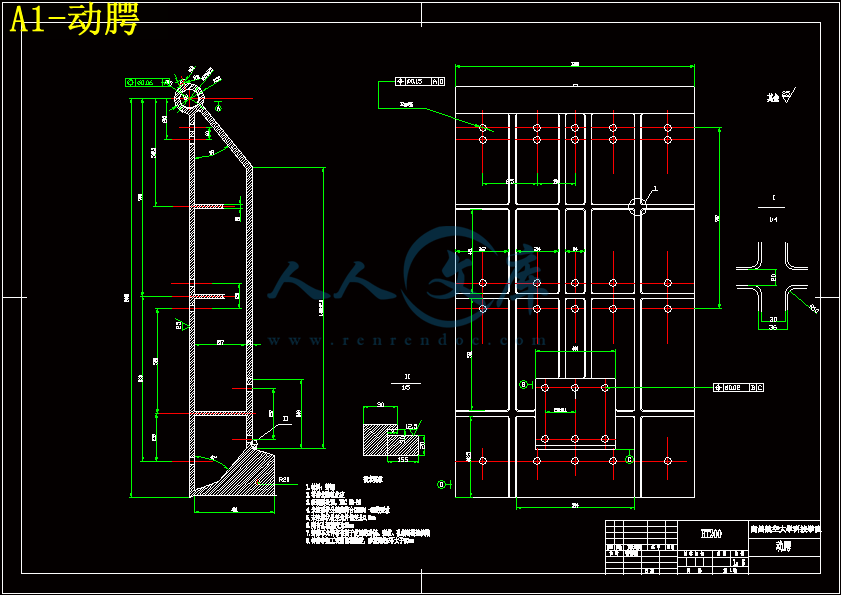
4.2动腭 15

4.3齿板的结构 16

4.4肘板 17

4.5调整装置 17

4.6保险装置 18

4.7机架结构 19

4.8传动件 20

4.9飞轮 20

4.10润滑装置 20

5 简摆腭式破碎机的主参数设计计算

5.1 机构参数 21

5.2 破碎力 25

5.3 功率的计算 27

5.4 主要零件受力计算 28

6 重要零件的设计和校核

6.1带轮的设计 30

6.2曲轴的设计计算 32

6.3 滑动轴承的设计计算 36

7 腭式破碎机的饿安装与运转

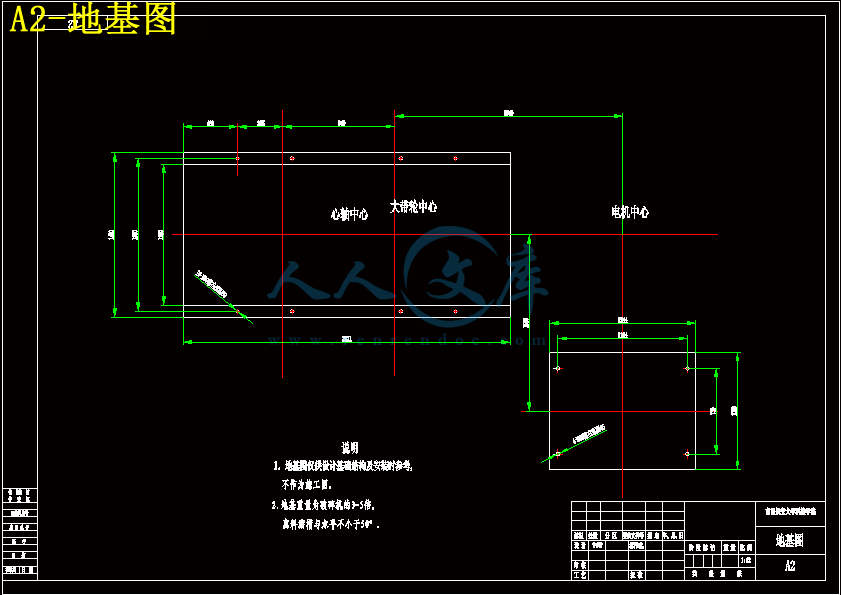
7.1破碎机的安装 38

7.2机架的安装 38

7.3连杆的安装 39

7.4肘板的安装 39

7.5动腭的安装 39

7.6齿板的安装 39

7.7破碎机的运转 40

8用对一个主要零件进行有限元分析

8.1solidworks软件介绍 41

8.2CosmosWorks功能和特点 41

8.3对曲轴的有限元分析 42

8.3变形结果 48

参考文献 49

致谢 50

摘要：破碎机械设备，属于矿山机械范畴。这这类机械设备在冶金、建材、化工、能源、交通建设、城市建设和环保等诸多领域有广泛的用途。简摆一般制成大型和中型的，复摆一般制成中型和小型的。简摆破碎机可以产生很大的破碎力，这是复摆破碎机所不能能、低能耗的新型颚式破碎机，从而大大提高了破碎机的性能，缩短了产品开比的，故在大型破碎机中一般用这种结构，复摆腭式破碎机的生产能力高于简摆腭式破碎机约30%，同时也因为过大的垂直行程，使得定、动腭衬板（齿板）磨损很快，大大降低了使用寿命。我国自50年代生产腭式破碎机以来，在破碎机设计方面经历了类比、仿制、图解法设计阶段，目前正向计算机辅助设计阶段过渡。国外从上世纪中后期开始利用计算机仿真技术对颚式破碎机机构、腔型、产量和磨损等进行优化，高性发周期，提高了产品的市场竞争力。

本文中所设计PEJ900X1200简摆颚式破碎机的设计要求为：破碎机偏心轴偏心距为25mm，连杆长度为1325mm左右，破碎腔设计为900×1200mm，破碎腔啮角20度，传动角为45～55度，动颚上端厚度为316mm，肘板长度为300～400mm，破碎机悬挂高度为100～160mm。腭式破碎机动颚水平行破碎腔啮角的大小直接关系到物料的受力状态，机架结构设计和破碎机产量，小的啮角有利于提高破碎机产量，利用先进破碎原理进行物料破碎，但破碎机高度将增加。所以根据经验值，本设计采用的啮角为20度。

关键词：简摆腭式破碎腔

1 概述

破碎机械是对固体物料施加机械力，克服物料的内聚力，使之碎裂成小块物料的设备。

破碎机械所施加的机械力，可以是挤压力、劈裂力、弯曲力、剪切力、冲击力等，在一般机械中大多是两种或两种以上机械力的综合。对于坚硬的物料，适宜采用产生弯曲和劈裂作用的破碎机械；对于脆性和塑性的物料，适宜采用产生冲击和劈裂作用的机械；对于粘性和韧性的物料，适宜采用产生挤压和碾磨作用的机械。

在矿山工程和建设上，破碎机械多用来破碎爆破开采所得的天然石料，使这成为规定尺寸的矿石或碎石。在硅酸盐工业中，固体原料、燃料和半成品需要经过各种破碎加工，使其粒度达到各道工序所要求的以便进一步加工操作。

通常的破碎过程，有粗碎、中碎、细碎三种，其入料粒度和出料粒度，如表1——1所示。所采用的破碎机械相应地有粗碎机、中碎机、细碎机三种。

表1—1 物料粗碎、中碎、细碎的划分（mm）

类别入料粒度出料粒度

粗碎

中碎

细碎 300～900

100～350

50 ～100 100～350

20～100

5～15

制备水泥、石灰时、细碎后的物料，还需进一步粉磨成粉末。按照粉磨程度，可分为粗磨、细磨、超细磨三种。

所采用的粉磨机相应地有粗磨机、细磨机、超细磨机三种。

在加工过程中，破碎机的效率要比粉磨机高得多，先破碎再粉磨，能显著地提高加工效率，也降低电能消耗。

工业上常用物料破碎前的平均粒度 D刁民破碎后的平均粒度d之比来衡量破碎过程中物料尺寸变化情况，比值i称为破碎比（即平均破碎比）

为了简易地表示物料破碎程度和各种破碎机的方根性能，也可用破碎机的最大进料口尺寸与最大出料口尺寸之比来作为破碎比，称为公称破碎比。

在实际破碎加工时，装入破碎机的最大物料尺寸，一般总是小于容许的最大限度进料口尺寸，所以，平均破碎比只相当于公称破碎比的0.7～0.9。

每各破碎机的破碎比有一定限度，破碎机械的破碎比一般是i=3～30。如果物料破碎的加工要求超过一种破碎机的破碎比，则必须采用两台或多台破碎机械串连加工，称为多级破碎。多级破碎时，原料尺寸与最终成品尺寸之比，称总破碎比，如果各级破碎的破碎比各是， … 。则总破碎比是

= …

由于破碎机构造和作用的不同，实际选用时，还应根据具体情况考虑下列因素；

1)物料的物理性质，如易碎性、粘性、水分泥沙含量和最大给料尺寸等；

2)成品的总生产量和级配要求、据以选择破碎机类型和生产能力；

3)技术经济指标，做到既合乎质量、数量的要求、操作方便、工作可靠，又最大限度节省费用。

全部文件.jpg

A0-装配图.gif

A1-动腭.gif

A2-大带轮.gif

A2-地基图.gif

A2-连杆.gif

A2-连杆体.gif

A2-曲轴.gif

A3-小带轮.gif

内容简介：: JOURNAL OF OPTIMIZATION THEORY AND APPLICATIONS: Vol. 6, No. I. 1970SURVEY PAPEROptimization of Structural Design I.W. PRAGER 3Abstract. Typical problems of optimal structural design are discussed to indicate mathematical techniques used in this field. An introductory example(Section 2) concerns the design of a beam for prescribed maximal deflection and shows how suitable discretization may lead to a problem of nonlinear programming, in this case, convex programming. The problem of optimal layout of a truss (Section 3) is discussed at some length. A new method of establishing optimality criteria (Section 4) is illustrated by the optimal design of a statically indeterminate beam of segmentwise constant or continuously varying cross section for given deflection under a single concentrated load. Other applications of this method (Section 5) are briefly discussed, and a simple example of multipurpose design (Section 6) concludes the paper.1. IntroductionThe most general problem of structural optimization may be stated as follows: from all structural designs that satisfy certain constraints, select one of minimal cost. Note that this statement does not necessarily define a unique design; there may be several optimal designs of the same minimal cost.Typical design constraints that will be considered in the following specify upper bounds for deformations or stresses, or lower bounds for load-carrying capacity, buckling load, or fundamental natural frequency. Both singlepurpose and multipurpose structures will be considered, that is, structures that are respectively subject to a single design constraint or a multiplicity of constraints.The term cost in the statement of the design objective may refer to the manufacturing cost or to the total cost of manufacture and operation over the expected lifetime of the structure. In aerospace structures, the cost of the fuel needed to carry a greater weight frequently overshadows the cost of manufacture to such an extent that minimal weight becomes the sole design objective. This point of view will be adopted in the following.In the first part of this paper, typical problems of optimal design will be discussed to illustrate mathematical techniques that have been used in this field. The second part will be concerned with a promising technique of wide applicability that has been developed recently. Throughout the paper, it will be emphasized that the class of structures within which an optimum is sought must be carefully defined if meaningless solutions are to be avoided. The fact will also be stressed that certain intuitive optimality criteria of great appeal to engineers do not necessarily furnish true optima. For greater clarity in the presentation of design principles, the majority of examples will be concerned with single-prupose structures even though multipurpose structures are of far greater practical importance.2. DiscretizationTo explore the mathematical character of a problem of structural optimization, it is frequently useful to replace the continuous structure by a discrete analog. Consider, for instance, the simply-supported elastic beam in Fig. 1. The maximum deflection produced by the given load 6P is not to exceed a given value To discretize the problem, replace the beam by a sequence of rigid rods that are connected by elastic hinges. In Fig. 1, onlyFig. 1. Discrete analog of elastic beam.three hinges have been introduced; but, to furnish realistic results, the discretization would have to use a much greater number of hinges. The bending moment itransmitted across the ith hinge is supposed to be related to the angle of flexure byi= (1) isiwhere is the elastic stiffness of the hinge. Since the beam is statically determinate, isthe bending moments at the hinges are independent of the stiffnesses ; thus,i is=5Ph= , =3Ph= , =Ph= . (2)11s22s33sIn the following, the angles of flexure , will be treated as small. In a design ispace with the rectangular Cartesian coordinates , i = 1, 2, 3, the nonnegative character of the angles of flexure and the constraints on the deflections at the hinges iudefine the convex feasible domain，， 0,1235 +3 + -6 /h 0,3 +9 -3 -6 /h 0, （3）123+3 +5 -6 /h 0，As will be shown in connection with a later example, the cost (in terms of weight) of providing a certain stiffness may be assumed to be proportional to this stiffness. The design objective thus is + + =Min or, by (2),1s235/ +3/ +1/ =Min (4)123Note that, for the convex program (3)-(4), a local optimum is necessarily a global optimum. This remark is important because a design that can only be stated to be lighter than all neighboring designs satisfying the constraints is of little practical interest. Note also that the optimum will not, in general, correspond to a point of design space that lies on an edge or coincides with a vertex of the feasible domain. This remark shows that the intuitively appealing concept of competing constraints is not necessarily valid. Suppose, for instance, that a design , , has been found for 1s23which = . If denotes a sufficiently small change of stiffness, the design 3u21s+ , - , , which has the same weight, might then be expected to have 1ss3deflection ，， satisfying , = , and all three stiffnesses 12u3u21ucould be decreased in proportion until the deflection at the first hinge has again the value . If this argument were correct, this process of reducing the structural weight could be repeated until the deflections at the hinges 1 and 2 had both the value &. In subsequent design changes, and would be increased by the same small amount 1s2while would be decreased by twice this amount to keep the weight constant. In this 3sway, it might be argued that the optimal design must correspond to a point on an edge or at a vertex of the feasible domain, that is, that, for the optimal design, two or three of the constraining inequalities must be fulfilled as equations. This concept of competing constraints, to which appeal is frequently made in the engineering literature, is obviously not applicable to the problem on hand.Minimum-weight design of beams with inequality constraints on deflection has recently been discussed by Haug and Kirmser (Ref. 1). Earlier investigations (see, for instance, Refs. 2-4) involved inequality constraints on the deflection at a specific point, for instance, at the point of application of a concentrated load. In special cases, where the location of the point of maximum deflection is known a priori, for instance, from symmetry considerations, a constraint on the maximum deflection can be formulated in this way. As Barnett (Ref. 3) has pointed out, however, constraining a specific rather than the maximum deflection may lead to paradoxical results. For example, when some loads acting on a horizontal beam are directed downward while others are directed upward, it may be possible to find a design for which the deflection at the specified point is zero. Since it will remain zero as all stiffnesses are decreased in proportion, the design constraint is compatible with designs of arbitrarily small weight.3. OptimalIn the preceding example, the type and layout of the structure (simply supported, straight beam) were given and only certain local parameters (stiffness values) were at the choice of the designer. A much more challenging problem arises when type and/or layout must also be chosen optimally.Figure 2a shows the given points of application of loads P and Q that are to be transmitted to the indicated supports by a truss, that is, a structure consisting of pin-connected bars, the layout of which is to be determined to minimize the structural weight. To simplify the analysis, Dorn, Gomory, and Greenberg (Ref. 5) discretized the problem by restricting the admissible locations of the joints of the truss to the points of a rectangular grid with horizontal spacing l and vertical spacing h (Fig. 2a). Optimization is then found to require the solution of a linear program. The optimal layout dependsFig. 2. Optimal layout of truss according to Dorn, Gomory, and Greenberg (Ref. 5).on the values of the ratios h/l and P/Q. Figures 2b through 2d show optimal layouts for h/l = 1 and P/Q = O, 0.5, and 2.0.For h/l = 1 and a given value of P/Q, the optimal layout is unique except for certain critical values of P/Q, at which the optimal layout changes, for instance, from the form in Fig. 2c to that in Fig. 2d. The next example, however, admits an infinity of optimal layouts that are all associated with the same structural weight.Three forces of the same intensity P, with concurrent lines of action that form angles of 120 with each other, have given points of application that form an equilateral triangle (Fig. 3 A truss that connects these points is to be designed for minimal weight, when an upper bound is prescribed for the magnitude of the axial 0stress in any bar.Figures 3b and 3c show feasible layouts. After the forces in the bars of these statically determinate trusses have been found from equilibrium considerations, the cross-sectional areas are determined to furnish an axial stress of magnitude in each 0bar. The following argument, which is due to Maxwell (Ref. 6, pp. 175-177), shows that the two designs have the same weight.Imagine that the planes of the trusses are subjected to the same virtual, uniform, planar dilatation that produces the constant unit extension e for all line elements. By the principle of virtual work, the virtual external work of the loads P on the virtual Wdisplacements of their points of applicationFig. 3. Alternative optimal designs.equals the virtual internal work = F of the bar forces F on the virtual iWelongations of the bars. If cross-sectional area and length of the typical bar are denoted by A and L, then F= A and = L. Thus,0= AL= V （5）i0where V is the total volume of material used for the bars of the truss. Now, depends only on the loads and the virtual displacements of their points of eWapplication but is independent of the layout of the bars; therefore, it has the same value for both trusses. If follows from = and (5) that the two trusses use the same eWiamount of material.If all cross-sectional areas of the two trusses are halved, each of the new trusses will be able to carry loads of the common intensity P/2 without violating the design constraint. Superposition of these trusses in the manner shown in Fig. 3d then results in an alternative truss for the full load intensity P that has the same weight as the trusses in Figs. 3b and 3c.Fig. 4. Alternative solution to problem in Fig. 3a.Figure 4 shows another solution to the problem. The center lines of the heavy edge members are circular arcs. The axial force in each of these members has constant magnitude corresponding to the tensile axial stress . The other bars are 0comparatively light. They are also under the tensile axial stress and are prismatic, 0except for the bars AO, BO, and CO, which are tapered.The bars that are normal to the curved edge members must be densely packed. If only a finite number is used, as in Fig. 4, and the edge members are made polygonal rather than circular, a slightly higher weight results. This statement, however, ceases to be valid when the weight of the connections between bars (gusset plates and rivets or welds) is taken into account.The interior bars in Fig. 4 may also be replaced by a web of uniform thickness under balanced biaxiat tension. While fully competitive as to weight, this design has, however, been excluded by the unnecessarily narrow formulation of the problem, which called for the design of a truss. In this case, the excluded design does not happen to be lighter than the others. However, unless the class of structures within which an optimum is sought is defined with sufficient breadth, it may only furnish a sequence of designs of decreasing weight that converges toward an optimum that is not itself a member of the considered class.Figure 5 illustrates this remark. The discrete radial loads at the periphery are to be transmitted to the central ring by a structure of minimal weight.If the word structure in this statement were to be replaced by the expressionFig. 5. Optimal structure for transmitting peripheral loads to central ring is truss rather than diskdisk of continuously varying thickness, the optimal structure of Fig. 5 would be excluded. Note that Fig. 5 shows only the heavy members. Between these, there are densely packed light members along the logarithmic spirals that intersect the radii at 45oThe problem indicated in Fig. 3a has an infinity of solutions, each of which contains only tension members. Figure 6 illustrates a problem that requires the use of compression as well as tension members and has a unique solution. The horizontal load P at the top of the figure is to be transmitted to the curved, rigid foundation at the bottom by a trusslike structure ofFig. 6. Unique optimal structure for transmission of load P to curved, rigid wall.minimal weight, the stresses in the bars of which are to be bounded by- and . The 0optimal truss has heavy edge members; the space between themis filled with densely packed, light members, only a few of which are shownin Fig. 6. Note that the displacements of the densely packed joints of thestructure define a displacement field that leaves the points of the foundation fixed. A displacement field satisfying this condition wilt be called kinematically admissible.There is a kinematically admissible displacement field that everywhere has the principal strains = / E and =- /E, where E is Youngs modulus. Indeed, if u 1020and v are the (infinitesimal) displacement components with respect to rectangular axes x and y, the fact that the invariant + vanishes furnishes the relation12+ =0，（6）where the subscripts x and y indicate differentiation with xuyrespect to the coordinates. Similarly, the fact that the maximum principal strain has the constant value e1 yields the relation4 * -( + )( + )=-4 （7）In view of (6), there exists xyvxyxvyu21a function such that,= , =- （ 8）Substitution of (8) into (7) uyvxfinally furnishes4 + =4 (9)Along the foundation are, u = v = 2xy2xy1O, which is equivalent to=0， =0 （10）where is the n nderivative of T along the normal to the foundation are.The partial differential equation (9) is hyperbolic, and its characteristics are the lines of principal strain. The Cauchy conditions (10) on the foundation arc uniquely determine the function , and hence the displacements (8), in a neighborhood of this arc.These displacements will now be used as virtual displacements in the application of the principle of virtual work to an arbitrary trusslike structure that transmits the load P to the foundation are (Fig. 6) and in which each bar is under an axial stress of magnitude %. With the notations used above in the presentation of Maxwells argmnent, = = . Here, = AeWiF0and , because no line element experiences a unit extension or 0/ELcontraction of a magnitude in excess of /E. Accordingly,0= F ( /E)V, (11) where V is again the total e2volume of material used in the structure.Next, imagine a second trusslike structure whose members follow the lines of principal strain of the considered virtual displacement field and undergo the corresponding strains. Quantities referring to this structure will be marked by an asterisk. Applying the principle of virtual work as before, one has = , but *=*eW*Fand = with correspondence of signs. Accordingly,*0A0/EL= = (12)In view of = , comparison of (11) eWF2*V*eWand (12) reveals that the second structure cannot use more material than the first.The argument just presented is due to Michell (Ref. 7), who, however, considered purely static boundary conditions and, consequently, failed to arrive at a unique optimal structure. The importance of kinematic boundary conditions for the uniqueness of optimal design was pointed out by the present author (Ref. 8).Figure 7 illustrates an important geometric property of the orthogonal curves of principal strain in a field that has constant principal strains of equal magnitudes and opposite signs. Let ABC and DEF be two fixed curves of one family. The angle c formed by the tangents of these curves at their points of intersection with a curve of the other family does not depend on the choice of the latter curve. In the theory of plane plastic flow, orthogonal families ofFig. 7. Geometry of optimal layout.curves that have this geometric property indicate the directions of the maximum shearing stresses (slip lines). In this context, they are usually named after Hencky (Ref. 9) and Prandtl (Ref. 10); their properties have been studied extensively (see, for instance, Refs. 11-13).Figure 8 shows the optimal layout where the space available for the structure is bounded by the verticals through d and B. Because the foundation arc is a straight-line segment, there are no bars inside the triangle dBC. Here again, the edge members are heavy, and the other members, of which only a few are shown, are comparatively light. The layout of these bars strongly resembles the trajectoriat system of the human femur (see, for instance, ReL 14, p. 12, Fig. 6). For further examples of Michell structures, see Refs. 15-16.4. New Method of Establishing Optimality CriteriaThe beam in Fig. 9 is built in at A and simply supported by B and C.Its deflection at the point of application of the given load P is to have the given value. The beam is to have sandwich section of constant core breadth B and constant core height H. The face sheets are to have the common breadth B,and their constant thicknesses H and H in the spans and are to be 1T21L2

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。