人人文库网 > 图纸下载 > 毕业设计 > 简摆腭式破碎机设计【8张CAD图纸和说明书】

翻译.doc

简摆腭式破碎机设计【8张CAD图纸和说明书】

资源目录

简摆腭式破碎机设计【8张CAD图纸和说明书】.zip

外文翻译

A0-装配图.dwg

A1-动腭.dwg

A2-地基图.dwg

A2-大带轮.dwg

A2-曲轴.dwg

A2-连杆.dwg

A2-连杆体.dwg

A3-小带轮.dwg

压缩包内文档预览：

编号：6039297 类型：共享资源大小：2.08MB 格式：ZIP 上传时间：2017-10-26 上传人：俊****计 IP属地：江苏

40
积分

版权申诉 word格式文档无特别注明外均可编辑修改；预览文档经过压缩，下载后原文更清晰！ 立即下载

关键词：: 破碎机设计 8张 cad 图纸说明书

资源描述：

1 概述

2 物料破碎及其意义

2．1 物料破碎及其意义 3

2．2 破碎物料的性能及破碎比 5

3 工作原理和构造

3.1 工作原理 10

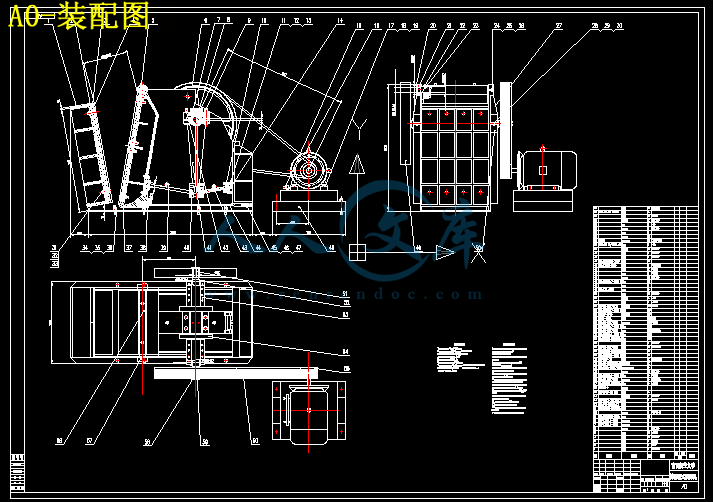
3.2简摆腭式破碎机的结构 11

4 主要零部件的结构分析

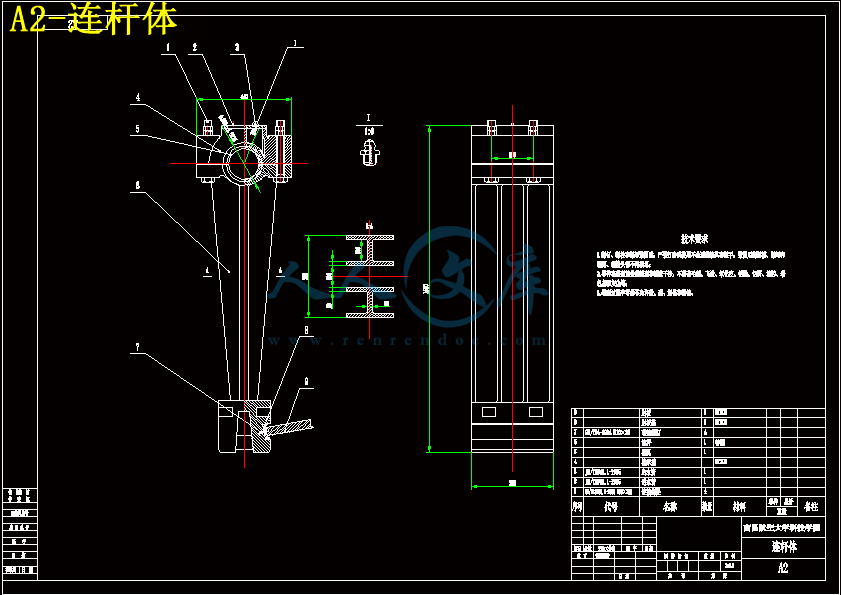
4.1连杆 14

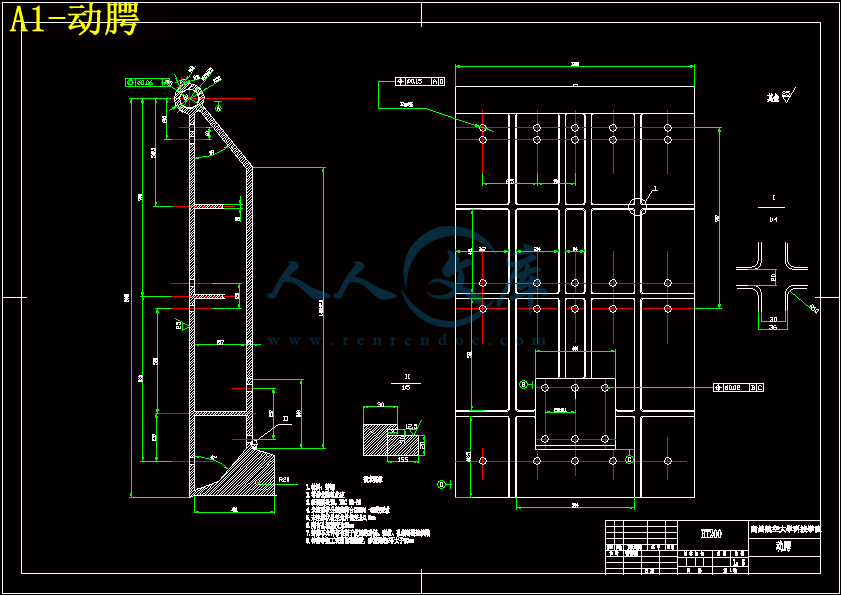
4.2动腭 15

4.3齿板的结构 16

4.4肘板 17

4.5调整装置 17

4.6保险装置 18

4.7机架结构 19

4.8传动件 20

4.9飞轮 20

4.10润滑装置 20

5 简摆腭式破碎机的主参数设计计算

5.1 机构参数 21

5.2 破碎力 25

5.3 功率的计算 27

5.4 主要零件受力计算 28

6 重要零件的设计和校核

6.1带轮的设计 30

6.2曲轴的设计计算 32

6.3 滑动轴承的设计计算 36

7 腭式破碎机的饿安装与运转

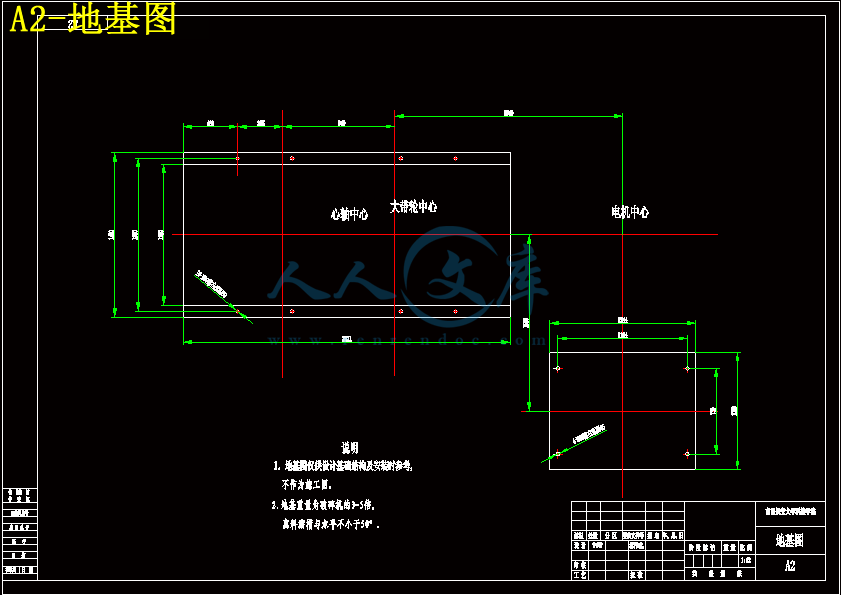
7.1破碎机的安装 38

7.2机架的安装 38

7.3连杆的安装 39

7.4肘板的安装 39

7.5动腭的安装 39

7.6齿板的安装 39

7.7破碎机的运转 40

8用对一个主要零件进行有限元分析

8.1solidworks软件介绍 41

8.2CosmosWorks功能和特点 41

8.3对曲轴的有限元分析 42

8.3变形结果 48

参考文献 49

致谢 50

摘要：破碎机械设备，属于矿山机械范畴。这这类机械设备在冶金、建材、化工、能源、交通建设、城市建设和环保等诸多领域有广泛的用途。简摆一般制成大型和中型的，复摆一般制成中型和小型的。简摆破碎机可以产生很大的破碎力，这是复摆破碎机所不能能、低能耗的新型颚式破碎机，从而大大提高了破碎机的性能，缩短了产品开比的，故在大型破碎机中一般用这种结构，复摆腭式破碎机的生产能力高于简摆腭式破碎机约30%，同时也因为过大的垂直行程，使得定、动腭衬板（齿板）磨损很快，大大降低了使用寿命。我国自50年代生产腭式破碎机以来，在破碎机设计方面经历了类比、仿制、图解法设计阶段，目前正向计算机辅助设计阶段过渡。国外从上世纪中后期开始利用计算机仿真技术对颚式破碎机机构、腔型、产量和磨损等进行优化，高性发周期，提高了产品的市场竞争力。

本文中所设计PEJ900X1200简摆颚式破碎机的设计要求为：破碎机偏心轴偏心距为25mm，连杆长度为1325mm左右，破碎腔设计为900×1200mm，破碎腔啮角20度，传动角为45～55度，动颚上端厚度为316mm，肘板长度为300～400mm，破碎机悬挂高度为100～160mm。腭式破碎机动颚水平行破碎腔啮角的大小直接关系到物料的受力状态，机架结构设计和破碎机产量，小的啮角有利于提高破碎机产量，利用先进破碎原理进行物料破碎，但破碎机高度将增加。所以根据经验值，本设计采用的啮角为20度。

关键词：简摆腭式破碎腔

1 概述

破碎机械是对固体物料施加机械力，克服物料的内聚力，使之碎裂成小块物料的设备。

破碎机械所施加的机械力，可以是挤压力、劈裂力、弯曲力、剪切力、冲击力等，在一般机械中大多是两种或两种以上机械力的综合。对于坚硬的物料，适宜采用产生弯曲和劈裂作用的破碎机械；对于脆性和塑性的物料，适宜采用产生冲击和劈裂作用的机械；对于粘性和韧性的物料，适宜采用产生挤压和碾磨作用的机械。

在矿山工程和建设上，破碎机械多用来破碎爆破开采所得的天然石料，使这成为规定尺寸的矿石或碎石。在硅酸盐工业中，固体原料、燃料和半成品需要经过各种破碎加工，使其粒度达到各道工序所要求的以便进一步加工操作。

通常的破碎过程，有粗碎、中碎、细碎三种，其入料粒度和出料粒度，如表1——1所示。所采用的破碎机械相应地有粗碎机、中碎机、细碎机三种。

表1—1 物料粗碎、中碎、细碎的划分（mm）

类别入料粒度出料粒度

粗碎

中碎

细碎 300～900

100～350

50 ～100 100～350

20～100

5～15

制备水泥、石灰时、细碎后的物料，还需进一步粉磨成粉末。按照粉磨程度，可分为粗磨、细磨、超细磨三种。

所采用的粉磨机相应地有粗磨机、细磨机、超细磨机三种。

在加工过程中，破碎机的效率要比粉磨机高得多，先破碎再粉磨，能显著地提高加工效率，也降低电能消耗。

工业上常用物料破碎前的平均粒度 D刁民破碎后的平均粒度d之比来衡量破碎过程中物料尺寸变化情况，比值i称为破碎比（即平均破碎比）

为了简易地表示物料破碎程度和各种破碎机的方根性能，也可用破碎机的最大进料口尺寸与最大出料口尺寸之比来作为破碎比，称为公称破碎比。

在实际破碎加工时，装入破碎机的最大物料尺寸，一般总是小于容许的最大限度进料口尺寸，所以，平均破碎比只相当于公称破碎比的0.7～0.9。

每各破碎机的破碎比有一定限度，破碎机械的破碎比一般是i=3～30。如果物料破碎的加工要求超过一种破碎机的破碎比，则必须采用两台或多台破碎机械串连加工，称为多级破碎。多级破碎时，原料尺寸与最终成品尺寸之比，称总破碎比，如果各级破碎的破碎比各是， … 。则总破碎比是

= …

由于破碎机构造和作用的不同，实际选用时，还应根据具体情况考虑下列因素；

1)物料的物理性质，如易碎性、粘性、水分泥沙含量和最大给料尺寸等；

2)成品的总生产量和级配要求、据以选择破碎机类型和生产能力；

3)技术经济指标，做到既合乎质量、数量的要求、操作方便、工作可靠，又最大限度节省费用。

全部文件.jpg

A0-装配图.gif

A1-动腭.gif

A2-大带轮.gif

A2-地基图.gif

A2-连杆.gif

A2-连杆体.gif

A2-曲轴.gif

A3-小带轮.gif

内容简介：: 优化结构设计W. PRAGER 3摘要。数学技术被应用在典型的优化结构设计问题这一领域。介绍一个关于一个杆的设计为了描述最大化绕度和显示怎样适当的离散化可能导致一个非线性的问题，在这种情况下的复杂的程序。最优布局已经被讨论了一段时间。一种新的建立最优标准的方法已经说明了被设计一个静不定梁或一个变截面的绕度在一个单一的集中压力下。其他的应用这个方法被简单的讨论，并且用一个多功能的设计的简单的例子来结束这份文件。1 。导言结构最优化的最普通的问题或许可以表述如下：从所有的满足某些限制的结构设计，选择其中一个最低成本的。注意这个声明并不定义一个唯一的设计;可能同时有几个最优化的设计有相同的成本。典型的设计将考虑满足变形或受力的最大约束，或者最小约束的承载能力，屈服载荷，或固有频率。单一的和多用途的结构都要被考虑，即是受单一因素或多重因素的约束。设计声明中的花费也许会参照到制造成本或总生产成本和生产中结构的寿命。在航天结构中，燃油成本需要执行最大的重量但最小的质量是他们设计的唯一目标，这个观点将要使用在下面文章。在这个文献的第一部分，优化设计的典型问题将用已经应用这个方面的数学技术来说明第二部分将要关注有广泛应用的有很大前途的最近发展的技术这整个文章，它强调具有最优整体结构是必须被仔细的定义没有意义的方案是要避免的。事实上还要强调指出某些直观的最优准则对工程师来说不一定提供真正的最优解。为了更清晰的介绍设计原则，大多数例子是关于单一约束的结构尽管多约束的结构是具有更大的实际意义。2 。离散去探索具有数学性质的最优化结构问题，这是经常有用的用一个分立模拟取代连续问题。考虑，例如，简直弹性梁在图。 1 最大偏转所产生的给予负荷6P 不会超过给定值。对于离散性问题，用一系列用弹性铰链连接的刚性棒取代梁。图 1.分立模拟弹性梁。在图 1 中，紧紧三个铰链已经被介绍了。但是，为了得到真实的结果，这个离散取决于铰链的数目。弯矩可以转换铰链数目 i 和角度的关系为 = iiisi(1)其中是弹性刚度的铰链。由于是静定梁，在铰链上的弯矩独立的刚度；is iis因此，=5Ph= , =3Ph= , =Ph= . (2)1122s33s接下来，弯曲角度将被视为最小。在一个直角坐标系的实际空间中 ,i ii=1,2,3,这个非负性质的弯曲角度和在铰链上的绕度定义凸可行域。iu，， 0,1235 +3 + -6 /h 0,3 +9 -3 -6 /h 0, （3）123+3 +5 -6 /h 0，作为接下来将要讲的例子，一组质量的刚度假定达到刚度的一定比例。这个设计即是 + + =Min 或，通过公式（2）1s235/ +3/ +1/ =Min (4)值得注意的是通过公式（3）-（4），一个局部优化对于整体优化必须的。这句话很重要因为刚刚开始的设计对于满足所有约束的相邻设计是没有什么实际价值的。也要注意到优化总体上不会对应到位于一个边的或恰好位于一个顶点区域的一个点的空间设计。这句话直观的表明冲突的约束不一定是有用的。假如，举个例子来说，设计 , , 条件 = .假如是刚度的最小变1s23u21s量，设计 + , - , ,拥有相同的质量的理想绕度为，，满足 1s23 1u233u, = 而且三个刚度降低一定的比例直到第一个铰链的绕度是。假2u 如这个探讨是正确的降低结构只来那个的过程能够被重复直到铰链 1 和 2 有相同的质量&。接下来设计的更改和都有想同的少量的增加而则降低两倍1s2 3s目的是保持质量常数。用这种方式，可能有争论关于；优化设计必须对应一个边上的一个点或者可行性区域上的顶点，由于优化设计，两三个不平等的约束就必须列方程。这冲突的约束通常会出现在工程界，显然用手是不能完成的。具有不平等约束绕度的最小重量梁的设计近期已经已经讨论了被 Haug and Kirmser（见 1）较早前调查（见，例如，参 2-4 ）在某一特定点所涉及的不等式约束对挠度，举例来说，在载荷集中在一个点上。在特殊情况下该点的最大绕度位置是已知的，举例来说，从对称的考虑，一个约束拥有最大绕度能够被指定通过这种方法。同样的 Barnett（见 3 ）已经指出，然而，约束一个具体而不是最大偏转的或许会出现自相矛盾的结果。举例来说，当一些载荷对横向是下降的然而其他的是上升的，也许会发现某些点的绕度是零。因为他仍然是零当所有的刚度都都以一定比例下降，这个设计的约束是相容性的任意小质量的约束。3 。布局优化在前面的示例，类型和布局结构（简单支持，直梁）被给予并且一些某些地方的参数（刚度值）是设计师选择的。一个更有挑战性的问题就是类型和/或布局也必须选择最佳的。数字显示，由桁架支持的给出点的应力载荷 P 和 Q ，即连接杆组成的结构，布局就是要去尽量减少重量。为了简化分析，Dorn, Gomory,and Greenberg（见 5 ）通过划分网格其横向间距 L 和垂直间距的 h 描述这个问题（图 2 a ）优化是接下来发现需要解决的线性规划。优化布局取决于质量的比例 h/L 和 P/Q=0,0.5,和 2.0.图.2 .优化布置的桁架根据多恩，戈莫里，格林伯格（见 5 ）。因为 h/L=1 和 P/Q 是一个给定数，优化值是唯一的除开某些临界值 P/Q，其中优化布局的变化，举例来说，从图 2c 到踢 2d。接下来例子，然而，承认一个无限大的优化布局是所有相关的拥有同样重量的结构重量。三个同样大小的作用力 P，彼此之间成 120 角，已经给出的点成等边三角形（图 3a）。这些连接点连接的构架用最小质量设计。当上界约束提供轴0向应力在任何杆。数据 3b 和 3c 是可行的布局。这些力作用在静定机构的杆上之后从平衡的角度考虑,每个杆件的横截面都会有一个大小的横向应力。0接下来讨论 Maxwell 的观点（见 6，PP 第 175-177 ）表明两个设计有相同的质量。设想飞机都是用相同的材料组成的，单位平面产生的张力达到 e 对所有的线性元素。通过虚拟的规律，这个杆件 P 上所有的点的位移所产生的虚拟功等价于内部虚拟功 = F 每个杆件受力为 F 力在杆方向的虚拟位移eWiW为 ,如果杆件的横截面积是 A 长度是 L，则有 F= A 和 = L 则有 0= AL= V （5）i00V 是使用的所有材料的体积。现在得到功取决于载荷和所有点的虚拟位移除e开独立布置图。 3 。选择最优设计。的杆件；他等价于两个机构如果下面 = 和（5 ）这两个构架使用相同数量的eWi材料。如果两个构架的横截面积都减半，每个新的构架能够驱动满载荷强度 P/2并且不违反设计约束.按图 3d 的方式叠加杆件另外用相同质量的构建按图 3d 和3c 叠加所有构架加载满载荷 P。图。 4 。替代解决问题，在图。第 3 a 图 4 显示的另一个解决问题的方法。所有重杆件的中心线是圆弧的。每个杆件的轴向力和他们的轴向应力有关0其他轻些的杆件。他们也根据轴向拉伸应力，除开杆件 AO,BO 和 CO，组成0圆锥。正常情况下杆件的边缘区域是受力的密集区域。如果紧紧是有限的数目被使用就像图 4 并且这些边缘是多变形而不是圆弧，这就是重量稍稍重一点点的结果。首先申明，然而，如果杆件连接件（节点板和铆钉或焊接）的质量被考虑其中这个就不是有效的。在图 4 中的杆件也许可以被有厚度统一材质均匀的杆件替代。然而质量是取胜之本，设计也是这样的，然而，设计构架的时候遇到的狭隘的问题要被排除。在这种情况下，被排除的设计将不会比其他的设计的质量更轻。然而，除开这一类对一个最优的进行有足够广度定义的，或许紧紧对一系列降低质量的设计进行融合一个最优的这不是考虑的范围之内图。 5 。优化结构转递周边荷载至中环环的桁架而非磁盘状图 5 对这句话进行了说明。在周边的离散的径向载荷等价于中央形成一个环状的小质量的构件。如果这个声明的结构将要被表达磁场形状的连续变厚度所取代，优化后的结构如图 5 要为排除。注意清楚看看图 5 他所显示的紧紧是质量大的成员。这些之间，质量轻些的成员之间关系是稠密的，他们之间是以螺线形状相45o交的。这个问题在图 3 中已经有一个解决方案，每个构件都紧紧是包含受力的杆件。图 6 说明了一个问题既要使用没有受力的也要使用受力的并且只有唯一解。上方的数据是横向载荷 P 会产生弯曲，底部的刚性结构可以看为是无限小的质量，在杆件上的应力应该在- 和之内。0这个最优的构架边缘杆件的质量较大；质量大的构件中间的构件的质量较轻，由图 6 表达。注意在位移密集的杆件连接处定义一个位移区域他的的基点固定。一个移动的受力区域都拥有这一规律即 = / E 和 =- /E 其中 E1020是弹性模量。事实上，如果 u 和 v 是位移分量类似于直角坐标系中的 x 和 y，那么 + 就是个常量有以下的关系即12 + =0，（6）xuyv其中 x 和 y 显示着不同的坐标关系。类似的，事实上最大的主应变 e1 拥有连续的线性关系4 * -( + )( + )=-4 （7）xyvxyxvyu21从公式（6）中可以看出，其中存在函数如下,xy= , =- （8）uyvx把公式（8）代入公式（7）中则有4 + =4 (9)2xy2xy1沿着根部弧有， = =0,则可以推到出uv=0， =0 （10）n其中是沿着根部弧的微变量。微分方程（9）是一个双曲线，其特点主应变是线性变化的。柯西条件在公式（10）中元素在根部是是独特的，并且和公式（8）位移也有关系图。 6 。在传输载荷 P 下弯曲和刚性壁的独特的优化结构这些位移现在将使用作为真正位移在虚功原理在一个任意的结构上其载荷P 传达到基座弧（图 6）并且每个连杆都在一个轴向应力为o 之下使用Maxwell 公式则有，可以得到 = = 其中 = A 并且 eWiFF0因为每个单位的拉伸或者压缩量超过 /E 就不是线性变化了，0/EL 0= F ( /E)V, (11)eW20其中 V 是所有材料的总体积。接下来，设想第二中结构它是由有规律线性应变的的连杆组成并且他要考虑到虚拟的移动区域和底部相应的应变涉及到结构的质量将要用星号标记。就像前面所讲的那样运用虚拟原理，最有 = ,但是 *= 并且 =*eW*F*0A*0/EL则有 = = (12)eW*F2*0/EV则可以看出 = ,比较表达式（11）和（12）则可以看出第二种方案的结构*e使用的材料要比第一种方案少。刚刚介绍的观点来自于 Michell（见 7），然而，是一个纯粹的静态的边界条件，因此不能达到一个独特的优化结构。对一个独特的优化涉及来说最重要的是运用运动学边界条件已经被作者指出（见 8）图。 7 。几何布局优化。图 7 说明了一个重要的具有几何性质的在有规律的应变和无规律的应变组成的区域种的正交曲线应变让由 ABC 和 DEF 组成的两个固定曲线。角度是由一个曲线上的切线和另外一个曲线上点的切线相交的夹角。在平移的理论下，正交的曲线他的几何性质可以表明他最大的剪应力（滑移线）的方向在这个背景下，它们通常后来被 Hencky (见. 9) and Prandtl (见. 10)命名；它们的结果已经被广泛的应用（见，例如，见。11-13）图。 8 。优化布置时，可用空间范围内垂直通过 A 和 B 。图 8 显示了最优空间的布局即可用的结构空间是垂直连线 A 和 B 之间的范围。因为这个固定支座弧是一个直线部分，在三角形 ABC 中间没有连杆。再次显示，他的边缘的杆件的质量重，其他的连杆紧紧一些并且质量轻。这些杆件不布局有些类似于人类的骨架的结构(see, for instance,ReL 14, p. 12, Fig. 6)。Michell 结构给出了更深一步的理解，参照。15-16.4 。新方法，建立优化准则图。 9 。梁展不断截面。在图 9 中的梁是建立在 A 上面的并且 B 和 C 只是给予了简单的支撑。承受载荷 P 的这一点的绕度的值是。这个梁有一个核心部分他的宽度是 B 并且它的高度是 H。这个梁他的宽度是 B 并且它们连续的厚度满足 H 和1TH 在和上这样的目的是尽量减少这个结构梁的质量由于他的核心面的2T1L2尺寸已经被定义了，尽量减少这个梁的质量也就意味着要尽量减少制约质量的尺寸。此外，由于厚度为横截面积的抗弯曲弹性刚度，其中 i=1,2,有iTis,其中 E 是杨氏模量，2/iisEBH(13)12WLs这个可能被视为尽量减少质量的方程。使得是从杆件上典型横截面到杆件最左边的距离，并且在这个横截面上的ix曲率和弯矩分别是和则的表达式可以写为如下ikiiMskP= = (14)Piiidx2iidx就是在 Li 进行微积分。在此框架内的问题，设计一个梁就是确定的值，i=1，2.假如和都满isisi足设计的约束（给出只），并且和假设载荷下给出的曲率，根据（14）Piki公式 = （15）2iiskdxiiskdx此外，曲率是约束变动的（即满足绕度的）根据，根据最小势能原理i is根据即is(16)2iikdxP2iiskdxP约去两边的在式子（16）中在根据式子（15）可得（17）0iisL这里（18）2(1/)iiikdx则就是每个单位平方米的曲率在上。假如iL(19)12从公式（17）和（13）得到其满足这设计另外设计的约束不能比刚刚满足is约束的设计更重。因此条件（19）是最优的，这个条件也是下面所要讲到的。is应用这个定义则有（20）iiisL设计的条件不应该比设计条件是的质量更重由下面公式得到is i（21）0i换个方面说，不等式（17）从最小势能原则得到（22）i, 和，将作为和的载体像坐标系。1212这个不等式（21）中不能位于第二和第四象限，并且这个不等式要求和是个非负的。现在，优化设计和他的平均曲率都是未知的但是是唯一的。换个方面来is讲，是受的值所限，因此当的方向被选择时其等级也所确定。此外，在isP这个最优化设计中的，他的结构质量将最接近最小质量。接近于边缘空间isi的相应的一半将被不等式（21）确定。假如和的坐标是非负的，那么和的坐标必须位于正常的一半空间内，因此，（19）是最优化的必要条件，这是根据 Sheu and Prager (见. 17).5。多用途的设计图。 11 。多用途的设计。

温馨提示:
1: 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享，仅供网友学习交流，未经上传用户书面授权，请勿作他用。