制订YD-65油锯右箱工序卡及镗铣结合面夹具设计
38页 14000字数+论文说明书+任务书+20张CAD图纸【详情如下】
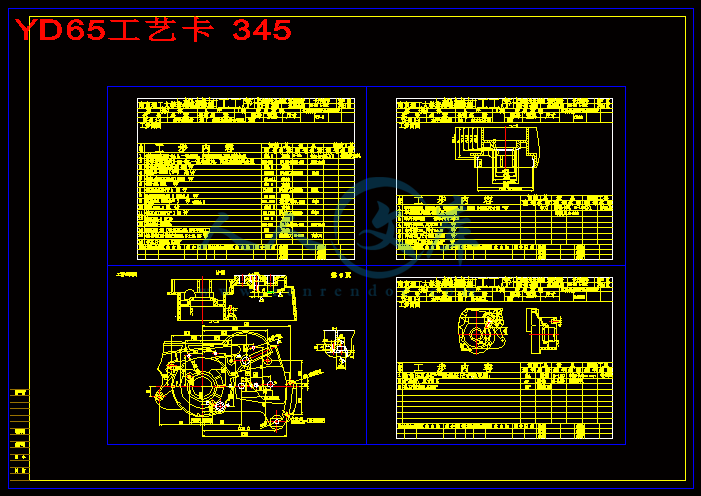














YD65工艺卡 345.dwg
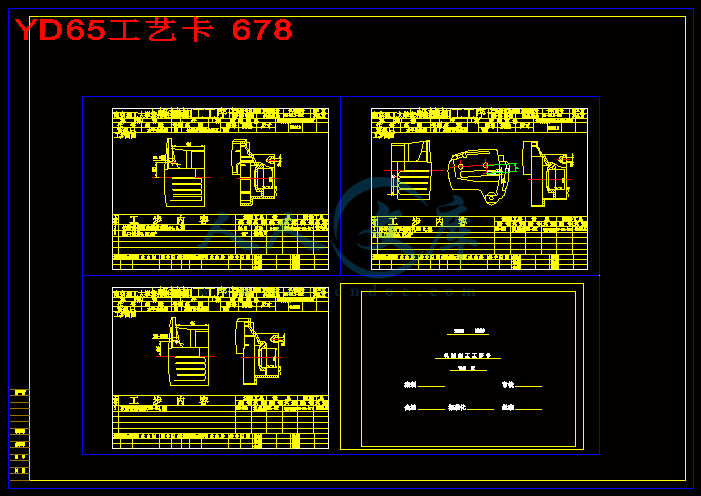
YD65工艺卡 678.dwg
YD65工艺卡12.dwg
任务书.doc
制订YD-65油锯右箱工序卡及镗铣结合面夹具设计开题报告.doc
制订YD-65油锯右箱工序卡及镗铣结合面夹具设计论文.doc
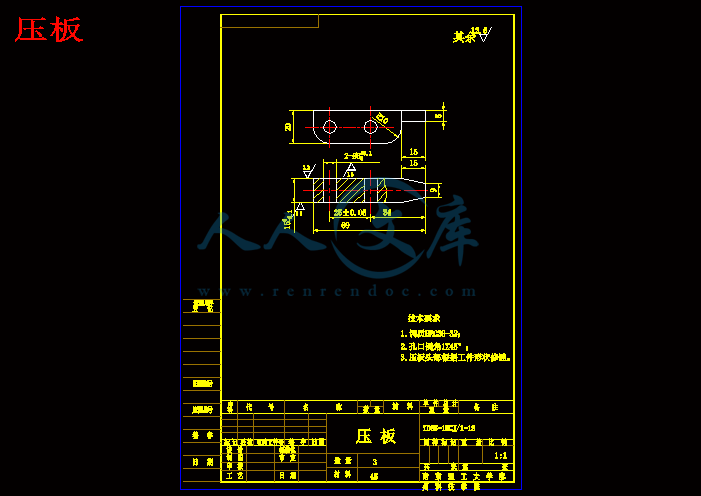
压板.dwg
压紧杆.dwg
堵头.dwg
外文翻译-- 利用三次样条函数.doc
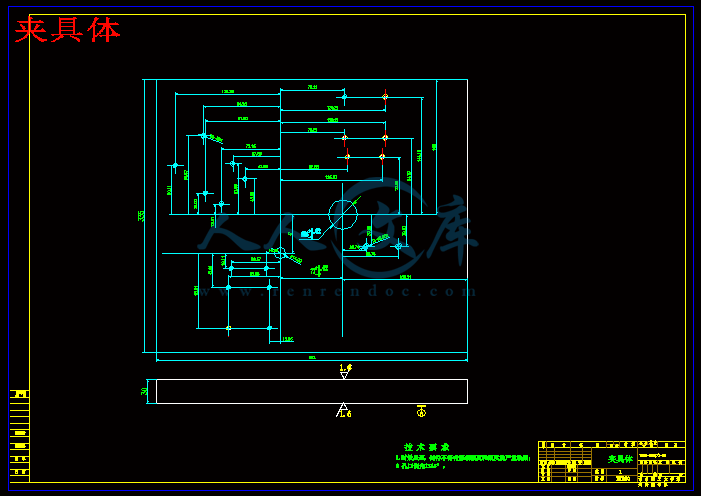
夹具体.dwg
夹具装配图.dwg
弹簧A.dwg
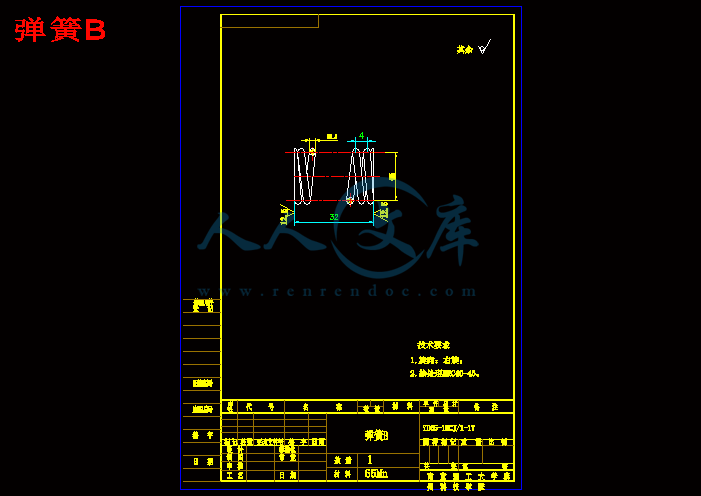
弹簧B.dwg
支座.dwg
支承座.dwg
支撑钉.dwg
气缸座.dwg
浮动支撑块.dwg
浮动锥环.dwg
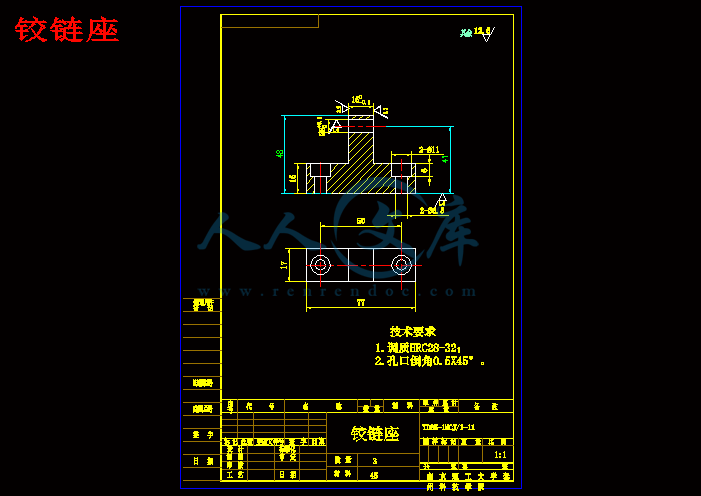
铰链座.dwg
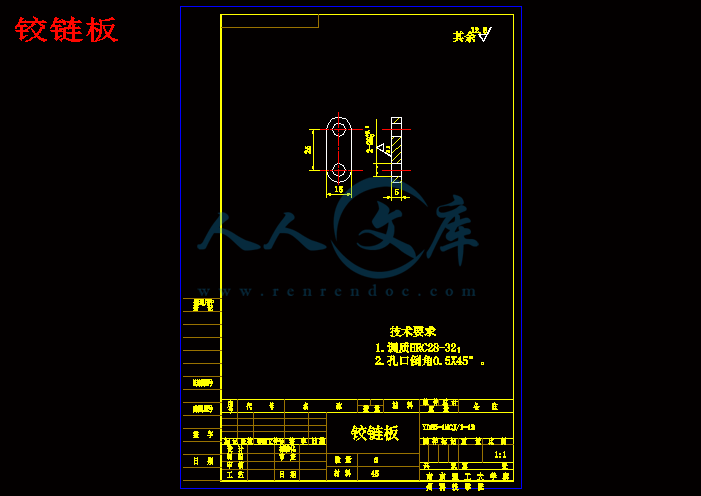
铰链板.dwg
销轴.dwg
锁紧楔块.dwg
目 录
1 引言 1
1.1 加工零件 2
1.2 机械加工工艺 2
2 零件的分析 3
2.1 零件的作用 3
2.2 零件的工艺分析 3
3 工艺规程设计 5
3.1 工艺规程的作用 5
3.2 毛坯的选择 5
3.3 基准面的选择 6
3.4 制定工艺路线 9
3.5 机械加工余量、工序尺寸及毛坯尺寸的确定 12
3.6 确定工件切削用量及基本工时 14
3.7 确定右半曲轴箱非结合面孔切削用量及基本工时 19
4 夹具设计 28
4.1 夹具的概述 28
5 专用夹具的提出 30
5.1 定位基准的选择 30
5.2 定位元件的选择 30
5.3 夹紧元件的选择 30
5.4 切削力及夹紧力的计算 30
5.5 定位误差的分析 31
5.6 夹具设计及操作简要说明 32
结束语 33
致谢 34
参考文献 35
毕业设计说明书(论文)中文摘要
组合机床是根据工件加工需要,以大量系列化、标准化的通用部件为基础,配以少量的专用部件,对一种或数种工件按预先确定的工序进行加工的高效专用机床。组合机床能够对工件进行多刀、多轴、多面、多工位同时加工;可完成钻孔、扩孔、镗孔、攻螺纹、铣削、车孔端面等工序。本文对TD65右箱体精镗孔的结构和工艺进行了分析,确定了机械加工工艺路线,制订出了零件的机械加工工艺规程。三图一卡的绘制:加工零件图,加工示意图,机床联系尺寸图和年生产率计算卡,以及零件的强度校核。
关键词 加工工艺 铸造工艺 工艺规程
毕业设计说明书(论文)外文摘要
Title The Composite Machining
Abstract
The process is the base of frock design、manufacturing、the method of machining and machining route. Its function is flowing: organizing produce, controlling quality, enhancing productivity, reducing cost, reducing produce periods, improving work conditions, etc. So, the process planning is the core part of produce. So the designing is also a basilica portion in machine process preparative and manufacture. This thesis is about the analysis with the craftwork and the structure of the speed governor tray , make sure the process route, establish the foundry process project and the process planning of the parts.
Keywords Group technology Foundry technology Process planning Fixture design
1 引言
毕业设计是学生在学校完成了大学四年的全部课程,并在进行了生产实习的基础上进行的一个教学环节,也是在校学习阶段,最后一个重要的教学环节,是完成工程师基本训练的一个必不可少的过程。通过毕业设计培养我们综合运用所学知识独立解决本专业一般工程技术问题的能力,树立正确的设计思想和工作作风。毕业设计是在毕业实习的基础上进行的,根据自己的设计课题,在毕业实习期间认真调查研究、搜索资料。
设计的目的和要求在于培养学生综合运用所学知识和技能去分析和解决机械工程实际问题的能力.熟练生产技术的工作的一般 方法,培养学生树立工程技术必备的全局观点,生产观点和经济观点。树立正确的设计思想和严肃认真的工作态度,培养学生调查研究,查阅技术文献资料,手册进行工程运筹,图样的绘制及编写技术文件的独立工作能力.
在做毕业设计中,通过到林海工厂的实际调研,对设计内容有了基本的了解,并仔细观察和了解各加工工序的加工过程,查阅了大量的资料,在梁红军高级工程师的指导下完成了设计任务,并编写了设计说明书。
就我个人而言,我希望通过这次课程设计对自己未来将从事的工作进行一次适应训练,从中锻炼自己分析问题、解决问题的能力,为今后的技术工作打下一个良好的基础。
机械加工工艺是规定产品或零件机械加工工艺过程和操作方法,是指导生产的重要的技术性文件。它直接关系到产品的质量、生产率及其加工产品的经济效益,生产规模的大小、工艺水平的高低以及解决各种工艺问题的方法和手段都要通过机械加工工艺来体现,因此工艺规程编制的好坏是生产该产品的重要保证和重要依据。
夹具结构设计在加深对课程基本理论的理解和加强对解决工程实际问题能力的培养方面发挥着极其重要的作用。利用更好的夹具可以保证加工质量,机床夹具的首要任务是保证加工精度,特别是保证被加工工件的加工面与定位面以及被加工表面相互之间的位置精度;提高生产率、降低成本,使用夹具后可以减少划线、找正等辅助时间,且易于实现多工位加工。扩大机床工艺范围,在机床上使用夹具可使加工变得方便,并可扩大机床工艺范围。减轻工人劳动强度,保证生产安全。为了让夹具有更好的发展,加快用高新技术改造和提升夹具技术水平的步伐,创建夹具专业技术网站,充分利用现代信息和网络技术,与时具进地创新和发展夹具技术[1]。
本次设计是制订YD-65油锯右箱工序卡及镗铣结合面夹具设计。设计正确的加工工艺路线。这次设计涉及到机床,机械加工工艺,工装夹具等机制专业的几乎所有的专业基础知识。是一次全面地,系统地检查自己在大学期间对专业知识学习的情况,在整个设计过程中做到严谨认真,一丝不苟的精神,尽量使自己的设计达到理想的水平,通过独立的查找资料,分析,计算完成方案设计,图纸设计和编写技术文件等,设计了这套比较完整的加工工艺路线,使自己对机制专业有了更深刻的认识。
由于时间短促,经验不足以及水平有限,本次设计难免许多不妥和错误之处,敬请批评指正,以便及时改正。
5.5 定位误差的分析
(1)定位元件尺寸及公差的确定
由于定位采用阶梯轴及圆销台定位,在加工过程中为保证平行度及其他尺寸要求,阶梯轴起到主要的作用。因此,只要阶梯轴的加工能够保证尺寸精确,定位误差就应该在符合加工误差范围内。夹具的主要定位元件为阶梯轴,该阶梯轴的尺寸与公差现规定为与本零件在工作时与其相配轴承的的尺寸与公差相同。
(2)工件在被加工的时候,使加工位置有一定转角误差。但是,由于加工是自由公差,故应当能满足定位要求,所以满足设计要求。
5.6 夹具设计及操作简要说明
如前所述,在设计夹具时,应该注意提高劳动生产率,而且夹具不是很庞大,同时也要考虑成本问题,所以我采用的是快速螺旋定位机构快速人工卡紧。当然在现生产条件允许的情况下,可以采用气动夹紧。本工序所设计的夹具是用阶梯轴及圆销台定位的,其中阶梯轴定位能保证较好的同轴度,只要阶梯轴尺寸加工准确,再利用辅助夹具,完全定位的目的可以达到。
在这里,如果夹具过于庞大的话,目前我们可以采取的措施有:一是提高毛坯的制造精度,使最大切削深度降低,以降低切削力;二是在可能的情况下,适当提高高压缩空气的工作压力,以增加气缸推力。本夹具总的感觉还是比较紧凑。
此专用夹具结构紧凑合理,定位及夹紧可靠,安装非常的方便,零件不是很多,使用时先将阶梯轴与孔配合,将螺栓扭紧,就可以按顺序加工了。
结束语
毕业设计是培养学生综合运用所学知识、发现、提出、分析和解决实际问题,锻炼实践能力的重要环节,是对学生实际工作能力的具体训练和参考过程。
回顾这次毕业设计,从选题到定稿,从理论到实践,在这段毕业设计期间里,可以说得是苦多于甜。通过本次毕业设计,不仅巩固了以前所学过的知识,而且学到了很多在书本上所没有学到过的知识。
对自己来说,收获最大的是方法和能力——那些分析和解决问题的方法与能力。在整个设计过程中,发现自己最缺少的是经验,没有感性的认识,空有理论知识,有些东西很可能与实际脱节。此次设计需要我们将学过的相关知识都系统地联系起来,从中暴露出自身的不足,以待改进。通过这次毕业设计,我懂得了理论与实际相结合是很重要的——只有理论知识是远远不够的,只有把所学的理论知识与实践相结合起来,从理论中得出结论,才能真正为社会服务,从而提高自己的实际动手能力和独立思考的能力。
在设计的过程中遇到问题,可以说得是困难重重。在设计的过程中也发现了自己的不足之处:对以前所学过的知识理解得不够深刻,掌握得不够牢固。通过这次毕业设计之后,又把以前所学过的知识重新温故。
这次毕业设计使我受益匪浅,为我今后的学习和工作打下了一个坚实而良好的基础。在此衷心感谢各位老师的帮助和指导。
致 谢
经过近四个月的忙碌和工作,本次毕业设计已经接近尾声,作为一个大学生生的毕业设计,由于经验的匮乏,难免有许多考虑不周全的地方,如果没有导师的督促指导,以及一起工作的同学们的支持,想要完成这个设计是难以想象的。
在这里首先要感谢我的指导老师。他平日里工作繁多,但在我做毕业设计的每个阶段,从开题报告到查阅资料,设计草案的确定和修改,中期检查,后期详细设计,装配草图等整个过程中都给予了我悉心的指导。我的设计较为复杂烦琐,但是老师们仍然细心地纠正图纸中的错误。除了敬佩老师的专业水平外,他的治学严谨和科学研究的精神也是我永远学习的榜样,并将积极影响我今后的学习和工作。
其次要感谢和我一起作毕业设计的同学们,他们在本次设计中勤奋工作,克服了许多困难来完成此次毕业设计,并分担了许多工作。如果没有他们的努力,此次设计的完成将变得非常困难。感谢学校图书馆的开放,让我们有足够的资料可供参考。还要感谢大学四年来所有的老师,为我们打下机械技术专业知识的基础;同时还要感谢所有的同学们,正是因为有了你们的支持和鼓励。此次毕业设计才会顺利完成。
通过毕业设计,使我对机械加工工艺这门课程进一步加深了理解。对于各方面知识之间的相互联系有了实际的体会。同时也深深感到自己初步掌握的知识与实际需要还有相当距离,还需在今后进一步学习和实践。本设计由于时间紧和对知识的掌握程度的限制,在设计上不很周详,许多应该考虑的因素,可能没在设计上体现出来。在这次设计过程中,我得到老师的精心指导和各方面的帮助,才能使设计得以顺利进行,借此我深表谢意最后感谢学院四年来对我的大力栽培!
参 考 文 献
[1] 大连组合机床研究所.组合机床设计[M]. 北京:机械工业出版社1976.
[2] 陈德生.机械制造工艺学[M].杭州:浙江大学出版社,2007.1
[3] 薛源顺.机床夹具设计[M]. 第二版,北京:机械工业出版社,2003
[4] 杨可桢,程光蕴. 机械设计基础[M]. 第四版,北京: 高等教育出版社,2004.
[5] 周海宝.提高机床夹具精度的实用方法[M]. 北京: 高等教育出版社,2000.
[6] 李昌年.机床夹具与制造[M]. 北京:机械工业出版社,2007.
[7] 秦国华,张卫红.机床夹具的现代设计方法[M]. 北京:航空工业出版社,2006.
[8] 王启平.机床夹具设计[M]. 哈尔滨:哈尔滨工业大学出版社,2005.
[9] 林钢,林慧国,赵玉涛.铝合金应用手册[M].北京:机械工业出版社,2006
[10] 金属机械加工工艺人员手册修订组.金属机械加工工艺人员手册[S].上海 科学技术出版社,1979.
[11] 马振福.机械制造技术[M].北京:机械工业出版社, 2005.
[12] 张佳.机械制造装备设计[M].北京:机械工业出版社,2003,8.
[13] 徐琏,邱宣怀.机械设计手册[S].北京:机械工业出版社,1991.
[14] 徐灏,邱怀宣,菜春源,汪恺,余俊.机械设计手册[S]. 北京:机械工业出版社,1989.
[15] 赵家齐.机械制造工艺学课程设计指导书[M].北京:机械工业出版社,2000.
[16] 徐琏,邱宣怀.机械设计手册[S].北京:机械工业出版社,1991.
 川公网安备: 51019002004831号
川公网安备: 51019002004831号