方程段 1 节 1在学习聚合物各种分子量时有 华

1、不同组分对聚合物分子量影响的讨论理优044班 10042777 杜征臻在学习聚合物各种分子量时，有这么一个结论：数均分子量对小分子组分比较敏感，而重均分子量对大分子组分比较敏感。下面对这个结论进行初步的讨论和证明。我对这个结论的理解是这样的：在两组相同的聚合物原始样品中，分别加入等量的小分子和大分子，并且它们的分子量和聚合物原始样品的分子量具有相同相对偏差。然后用聚合物样品分子量相对于原始样品分子量的相对变化来衡量组分对其敏感度。此外，对于等量也有不同的理解，可以理解为等物质的量，也可以理解为等质量。下面先对数均分子量的影响进行讨论。1 组分对聚合物数均分子量的影响1.1 理解为等物质的量设有

2、聚合物原始样品，其数均分子量为，共有，加入分子量为的组分。则加入后样品数均分子量变为用来衡量新加组分分子量和聚合物原始样品数均分子量之间的相对偏差，用来衡量聚合物样品前后数均分子量得相对偏差。则由此可见，当理解为等物质的量时，对于数均分子量而言，无论是大分子组分还是小分子组分，只要相对偏差不变，即在相同相对偏差的情况下，他们对聚合物样品数均分子量的变化的贡献是一样的，就是说在此种前提下，对数均分子量而言，大分子组分和小分子组分是同样敏感的。1.2 理解为等质量设有聚合物原始样品，其数均分子量为，共有，加入分子量为的组分。则由(0.2)可得若加入的是小分子组分，则由的定义可得：，代入方程(0.3

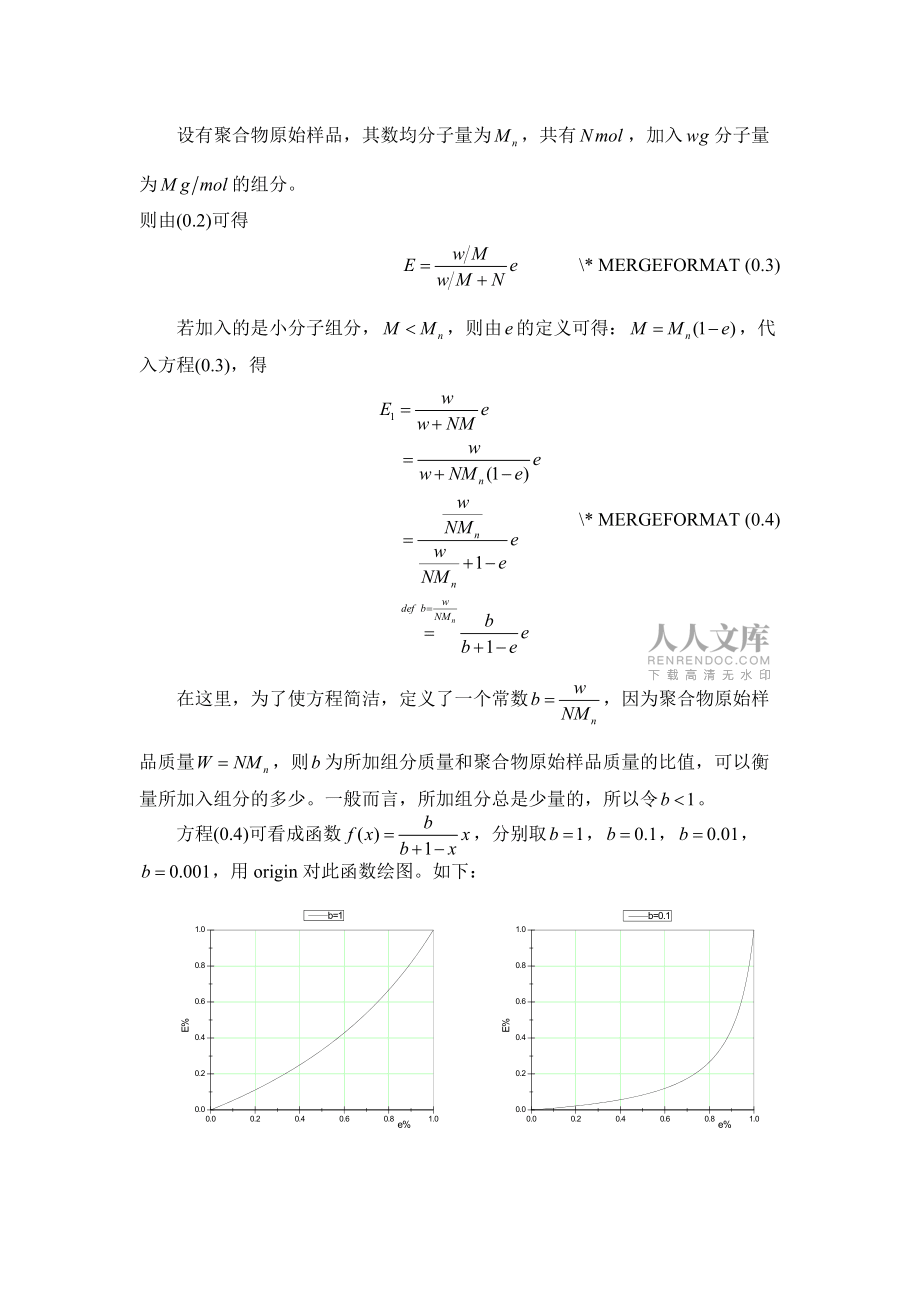
3、)，得在这里，为了使方程简洁，定义了一个常数，因为聚合物原始样品质量，则为所加组分质量和聚合物原始样品质量的比值，可以衡量所加入组分的多少。一般而言，所加组分总是少量的，所以令。方程(0.4)可看成函数，分别取，用origin对此函数绘图。如下： 由图可见，随着的增大，也增大，并且和加入组分质量有一定的关系。当加入组分和聚合物原始样品相当时，随近乎线性的变化，但是随着加入组分质量的减少，随的变化有了显著的改变。当较小时，即所加组分的分子量偏离程度较小时，几乎没有什么变化，但是当超过某一个值后，随的变化非常巨大，在图上表现为陡直的一条线。在图上可见，这个值随着的变小而增大，且逐渐接近1。若加入的

4、是大分子组分，则由的定义可得：，代入方程(0.3)，得在这里，同样定义了一个常数，具有和上述相同的意义。方程(0.5)可看成函数，分别取，用origin对此函数绘图。如下：由图可见，随着的增大，也增大，在较小时，有较大的变化，当时，随的变化就已经很小了。并且有一个极限，无论怎么变化，仍旧小于这个极限，这个极限和相等，当在时，已经相当接近这个极限了。接下来做一个比较，定义即在相同的和下，比较数均分子量对大分子组分的敏感度和对小分子组分的敏感度的大小。仍取，用origin对此函数绘图。如下：由图可见，在相同的下，随着的增大，始终为一负值，在开始减小较慢，但是减小速度逐渐增大，对是一个凸的增函数，不

5、存在最大值。并且图形形状随着的减小有了很大的变化，当较小时，图形突变非常明显，当超过某一个值后，随陡直的下降，这个值随着的变小而增大，且逐渐接近1。由此可说明对数均分子量而言，就以等质量理解，其对小分子组分的敏感性要高于对大分子组分的敏感性，且这一关系不随所加组分的不同而改变，并且，所加组分分子量相对于聚合物原始样品数均分子量的相对偏离程度越大，其敏感性差异也越大，此差异随着偏差的增大而加速增大。这些结论都可以从对上图的分析得到。2 组分对聚合物重均分子量的影响2.1 理解为等质量设聚合物原始样品的重均分子量为，有，加入分子量为的组分。则同样定义和来衡量组分分子量相对原始样品重均分子量的相对偏

6、差和重均分子量变化的相对程度。则由此可见，当在聚合物原始样品中加入等质量的大分子组分和小分子组分时，只要他们的相对偏差相同，对聚合物样品中重均分子量的影响是同值异号的，即在此种前提下，重均分子量对大分子组分和小分子组分是一样敏感的。2.2 理解为等物质的量设聚合物原始样品的重均分子量为，有，加入分子量为的组分。则由方程(0.8)可得若加入的是小分子组分，则由的定义可得：，代入方程(0.9)，得在这里，为了使方程简洁，同样定义了一个常数，并且可以这样理解，因为，那么是不是可以把也理解为具有类似意义的一个衡量聚合物样品所含链段数目的物理量呢？根据其形式，可以称它为重均分子摩尔数。那么就是表示聚合物

7、的量和加入组分的量的比值，衡量加入组分的多少。方程(0.10)可看成函数，分别取，用origin对此函数绘图。如下：由图可见，随着的增大，先增大后减小，存在一有个极大值，并且随着的增大，即所加组分的减少，对的影响也显著减小。若加入的是大分子组分，则由的定义可得：，代入方程(0.9)，得在这里，同样定义。方程(0.11)可看成函数，分别取，用origin对此函数绘图。如下： 由图可见，随着的增大，近乎线性的增大，不存在一个极大值，同时随着的增大，即所加组分的减少，对的影响也显著减小，但相比于小分子而言，下降的没那么快。接下来做一个比较，同样定义即在相同的和下，比较重均分子量对大分子组分的敏感度和

8、对小分子组分的敏感度的大小。仍取，用origin绘图。如下： 由图可见，在相同的下，随着的增大，始终为一正值，在开始增长较慢，但是增长速度逐渐增大，对是一个凹的增函数，不存在最大值。由此说明对重均分子量而言，就以等摩尔量理解，其对大分子组分的敏感性要高于对小分子组分的敏感性，且这一关系不随所加组分的不同而改变，并且，所加组分分子量相对于聚合物原始样品重均分子量的相对偏离程度越大，其敏感性差异也越大，此差异随着偏差的增大而加速增大。这些结论同样都可以从对上图的分析得到。3 补充不在上述讨论范围内的情况在上述的讨论中，都默认了这么一个事实，所加组分的量小于聚合物原始样品的量，接下来讨论一下所加组分

9、的量大于聚合物原始样品的量这一情况，即讨论和的情况。在等物质的量理解的数均分子量和等质量理解的重均分子量的讨论中，和的值是无意义的，无论和取何值，他们对大分子组分和小分子组分的敏感度是相同的，也只是对敏感度的大小有所影响。3.1 在等质量理解的数均分子量讨论中在此，所加组分质量大于聚合物原始样品的质量，即为的情况。首先讨论小分子组分的情况，同样方程(0.4)可看成函数，分别取，用origin对此函数绘图。如下：由图可见，对照的曲线，随着的增大，和之间的线性关系越来越明显。由于和所加小分子组分分子量之间是线性变化的，可见随着的增大，和也体现出了一种线性关系，联系到实际，说明随着所加小分子组分质量

10、的增大，样品前后数均分子量的变化渐渐地和原始样品数均分子量无关而更多地依赖于所加小分子组分的分子量。接下来讨论大分子组分的情况，同样方程(0.5)可看成函数，分别取，用origin对此函数绘图。如下：可见，这三条曲线形状和的那四条曲线类似，都有一个极限，无论怎么变化，仍旧小于这个极限，这个极限仍和相等。说明对大分子组分而言，加入的质量对聚合物数均分子量没有质的影响。但是随着的增大，为了能够明显接近那个极限，所需的也不断增大，和的增大保持一致的步调。即所加大分子组分分子量要远大于原始样品的数均分子量。同样在的条件下进行比较，取，对方程(0.6)用origin绘图。如下： 由图可见，对数均分子量而

11、言就以等质量理解其对小分子组分的敏感性要高于对大分子组分的敏感性这一结论不变，但是对照的曲线，发现那个突变值不再明显存在。同时随着的增大，对的影响也越来越小。3.2 在等物质的量理解的重均分子量讨论中在此，所加组分物质的量大于聚合物原始样品的物质的量，即为的情况。首先讨论小分子组分的情况，同样方程(0.10)可看成函数，分别取，用origin对此函数绘图。如下： 由图可见，对照的情况，发现区现有了明显的突变，突变现象在较小的情况下尤为明显。在突变前，随着近乎线性的变化，说明当所加小分子组分的物质的量大于原始样品的物质的量时，样品的重均分子量基本上只与所加小分子组分分子量有关，只有当所加小分子组

12、分的分子量特别小的时候才会打破这一规律。而过了突变点，非常迅速的降为零。并且这个突变点对应的随着的减小逐渐接近1。接下来讨论大分子组分的情况，同样方程(0.11)可看成函数，分别取，用origin对此函数绘图。如下：由图可见，对照的情况，对的线性关系也随着的减小越来越接近。但是，随着的减小，即所加组分的增多，对的影响不像的相反情况那样，虽然有所增大，但这增大的幅度根不能和在的情况中的下降相提并论。同样在的条件下进行比较，用origin对方程(0.12)绘图。如下：由图可见，说明对重均分子量而言，就以等摩尔量理解，其对大分子组分的敏感性要高于对小分子组分的敏感性这一结论不便，但是对照的情况，和的关系有了较大的不同，出现了一个突变点，这个点在较小的情况下尤为明显。在小于这个突变点的情况下，其对大分子组分的敏感性仅略大于对小分子组分的敏感性，两者近乎相等，而在大于这个突变点时，两者敏感性差异显著增加。这个突变点对应的随着的减小逐渐接近1。4 结论通过以上的讨论，可以得出以下几个结论：1 当以等物质的理解时，对数均分子量而言，大分子组分和小分子组分是同样敏感的；而对重均分子量而