福建专版2024春七年级数学下册第四章三角形素养集训1与三角形的高角平分线有关的计算模型作业课件新版北师大版

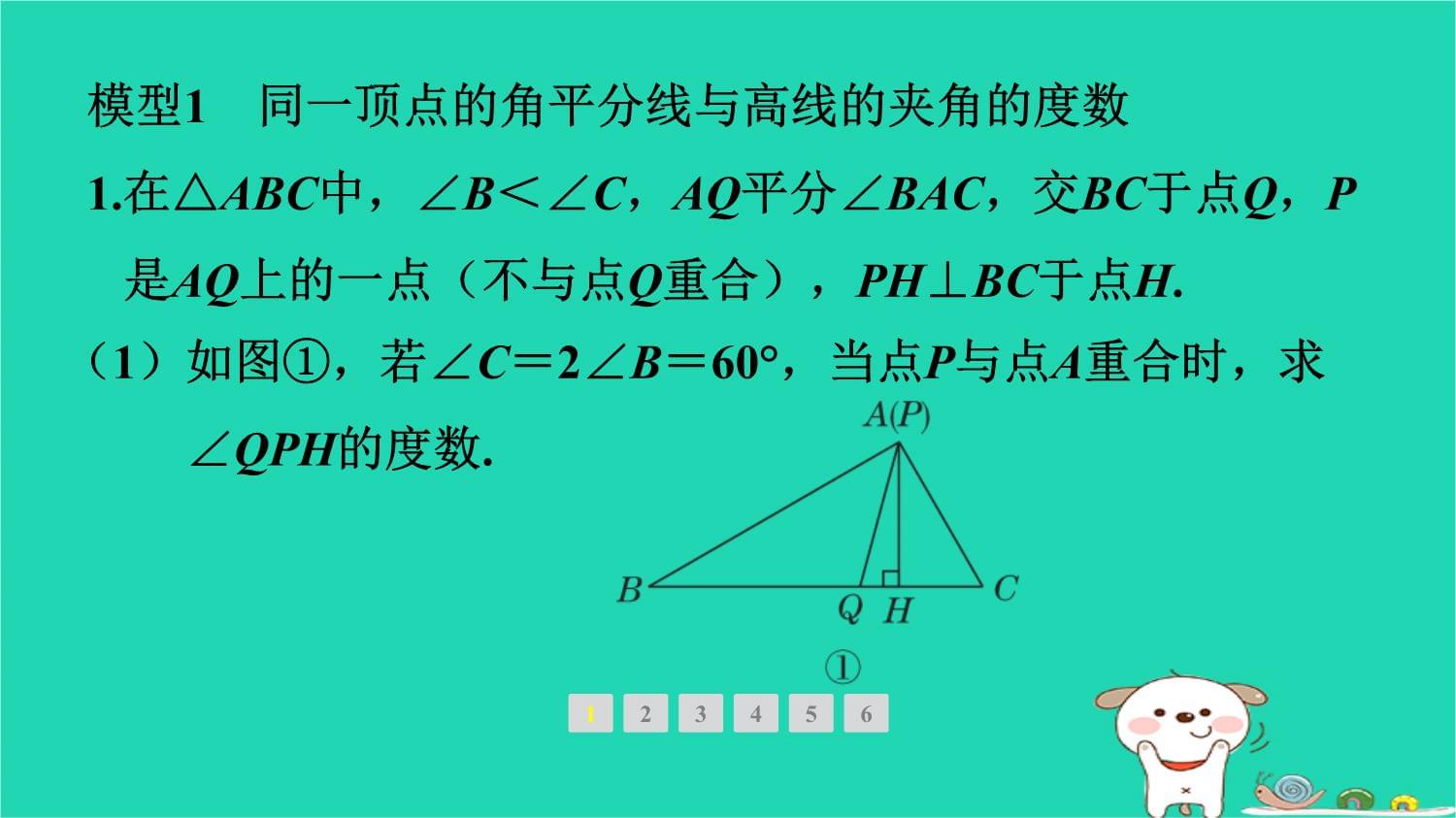
第四章三角形素养集训1.与三角形的高、角平分线有关的计算模型模型1同一顶点的角平分线与高线的夹角的度数1.在△ABC中，∠B＜∠C，AQ平分∠BAC，交BC于点Q，P是AQ上的一点（不与点Q重合），PH⊥BC于点H.123456（1）如图①，若∠C＝2∠B＝60°，当点P与点A重合时，求

∠QPH的度数.

123456（2）如图②，当△ABC是锐角三角形时，试探索∠QPH，

∠C，∠B之间的数量关系，并说明理由.模型1同一顶点的角平分线与高线的夹角的度数1.在△ABC中，∠B＜∠C，AQ平分∠BAC，交BC于点Q，P是AQ上的一点（不与点Q重合），PH⊥BC于点H.123456解：（2）过点A作AG⊥BC于点G，则∠PHQ＝∠AGQ＝90°，所以PH∥AG，所以∠QPH＝∠QAG.设∠QPH＝∠QAG＝x，因为AQ平分∠BAC，所以∠BAQ＝∠QAC＝x＋∠GAC.因为∠AQH＝∠B＋∠BAQ，∠AQH＝90°－x，所以∠BAQ＝90°－x－∠B.所以x＋∠GAC＝90°－x－∠B.123456

123456模型2不同顶点的角平分线与高线求角度2.如图，在△ABC中，CD是∠ACB的平分线，高AE与CD相交于点O，∠BAC＝70°，∠ACB＝60°.求：解：（1）因为∠BAC＝70°，∠ACB＝60°，所以∠B＝180°－∠BAC－∠ACB＝180°－70°－60°＝50°.（1）∠B的度数.123456（2）∠AOD的度数.

模型2不同顶点的角平分线与高线求角度2.如图，在△ABC中，CD是∠ACB的平分线，高AE与CD相交于点O，∠BAC＝70°，∠ACB＝60°.求：1234563.如图，在△ABC中，AD是高，BF是角平分线，AE，BF交于点O.若∠ABC＝50°，∠DAE＝10°，求∠AOB的度数.123456

所以∠AOB＝180°－∠ABF－∠BAE＝180°－25°－30°＝125°.123456模型3两条高线与一内角平分线求角度4.如图，在△ABC中，AD是角平分线，AE和BF是高，并且∠CBF＝∠DAE＝2∠ABF，求△ABC的各个内角的度数.123456

123456所以∠CAE＝∠DAC－∠DAE＝90°－7x.因为BF是△ABC的高，所以∠BFC＝90°＝∠AEC，所以∠EAC＋∠C＝90°，∠FBC＋∠C＝90°，所以∠EAC＝∠FBC，所以90°－7x＝2x，解得x＝10°，所以∠ABC＝3x＝30°，∠BAC＝2（90°－5x）＝80°，所以∠ACB＝180°－∠ABC－∠BAC＝70°.123456模型4两内角平分线求角度5.如图，在△ABC中，BE，CD分别为其角平分线且交于点O.（1）当∠A＝60°时，求∠BOC的度数.123456

123456模型4两内角平分线求角度5.如图，在△ABC中，BE，CD分别为其角平分线且交于点O.（2）当∠A＝100°时，求∠BOC的度数.123456

123456模型4两内角平分线求角度5.如图，在△ABC中，BE，CD分别为其角平分线且交于点O.（3）当∠A＝α时，求∠BOC的度数.123456

123456模型5求两外角平分线的夹角的度数6.已知：如图，△ABC两个外角的平分线BP