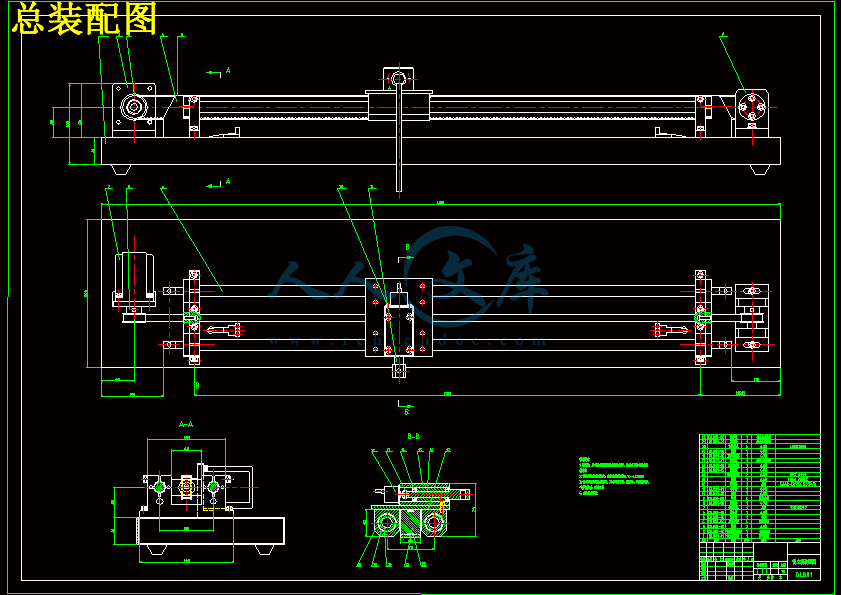
直线倒立摆的稳定控制算法设计【1张CAD图纸和说明书】
收藏
资源目录

压缩包内文档预览:
编号:6044489
类型:共享资源
大小:2.72MB
格式:ZIP
上传时间:2017-10-30
上传人:俊****计
认证信息
个人认证
束**(实名认证)
江苏
IP属地:江苏
40
积分
- 关 键 词:
-
直线
倒立
稳定
不乱
控制
节制
算法
设计
cad
图纸
以及
说明书
仿单
- 资源描述:
-


- 内容简介:
-
倒立摆的控制最合适的算法摘要本文的主要内容是 PID 调节器三种算法之间的比较。在这种情况下调节来自于所需垂直位置参数的偏差。调节器的结构和自动驾驶仪是相同的,都用于飞机俯仰角稳定。三种不同的结构的算法描述和这些结构之间不同的比例、积分和微分的增益是相互连接的。目标是使倒立摆能够找到最合适的算法结构。使之获得最好的系统的稳定性,稳定的角度范围宽,结构比较简单,没有超出规定的输入的局限性。关键词:倒立摆;推力矢量喷管;PID 调节器;自动驾驶仪1 引言倒立摆是一个典型的不稳定系统的例子,它被广泛用作测试控制算法(PID 控制器、神经网络、模糊逻辑等)的基准。本系统研究了在火箭起飞后的弹动力学,或者是在低动态压力不稳定的条件下推力矢量飞机飞行的条件。火箭的控制问题主要是使它保持在一个垂直的状态上当它的火箭加速时 1。倒立摆的摆角位置通过输入力来控制。在这种情况下,控制力是在矢量喷管的系统中产生的,在那里力和喷管偏转是成正比的。位置限制(20) 、速率限制(60 度/秒)和喷嘴动力学通过第二阶传递函数都被表示出来 2,在之后系统的模型向量喷嘴也被简要的描述出来。对这个倒立摆模型的非线性系统进行分析得到:222cosdxdMmlmlFttt(1)22sinxJllltt(2)其中 M小车的质量,m-倒立摆摆杆质量,L摆杆转动轴心到杆质心的长度,J-摆杆惯量,偏离垂直位置角度,X车位置坐标, g-重力加速度,F输入力。通过这些参数,可以得到系统的实际模型。该系统将用于所选择的控制系统的最终的非线性分析。方程(3) 为系统的传递函数,它是利用控制器的设计和调节器的参数设置来 对系统进行分析的: 52 221,80936nlsKJmUwssg (3)其中 K增益的系统,w n固有频率系统。这个函数很容易分析,可以看出 PID 调节器设计也不复杂。2 第一算法第一种算法描述的结构如下 3:zFsPsDs (4)F(s)-倒立摆所受外界作用力; Z(s)所需的 角度值;P ,D 调节器的系数。这种自动驾驶仪的结构包括两个循环外部和内部,如图 1 所示:图 1 第一算法的结构传递函数的内循环是:2221ooKswsDw(5)和整个系统的传递函数:22()z osKPs(6) 通过对 P、D 参数的计算及方程(6)得出:22spspw(7)从以往的公式,你可以找到相似飞机的短周期模式和相同的标准,短期内阻尼 sp 和频率 wsp 是可用的为这个目的,标准的短周期阻尼和频率根据4 ,5, 6是:0.351.;sp 1/secspwrad把方程(6)和表达式 (7)合并得:222()ospspKDP系数 D 可以计算:1spJwkgmsl(8)和系数 P:22spJDgksl(9)图 2 显示了阶跃响应,输入信号最终值阶跃函数为:/ 10。这个值是从方程的近似计算(1)和(2)得到的。系数 P 值为: P = 461049 和系数 D 为:D = 312133。图 2 角的时间响应你可以看到图 3,当 t = 0 的输入力超过这个结构限制时,它将不可用于进一步的设计。图 3 输入力的响应时间3 第二算法第二个算法给出了跟踪控制法 【3】 : zPsIFsDs(10)I 系数的选择和 PID 调节器的积分系数及其他参数的选择是一样的,如公式(4)。自动驾驶仪的结构如图 4 所示。图 4 第二算法的结构该模型由2循环也从内在和外在循环及传递函数中给出了有效的内部循环方程(5)。包括外层循环,最终的转移函数是:322z osKPsIDwI(11)第三阶系统的二项标准的形式描述了所需的时间响应 【3】 :323zzzssWz 是期望值的自然频率。P,I,D 系数:223zJPwmgksl(12)33zIsl(13)1zJDwkmgsl(14)时间的调节可以通过使用公式近似计算为:7secrzt(15)阶跃响应如图5所示,PID 调节器参数:P = - 1085315,8;I= 624267;D = 468200。它可以观察到图5的超调。尽量调整 P,I 和 D 系数来消除超调。对于不同的 Z 系数值如表 1所示。表1 不同的 Wz 系数值图5 角时间响应从图6中,可以看出超调量和 Z 值之间的关系。如果 Z 值增加,超调量减少,反之亦然。图6 角的时间响应你可以看到在图7中,输入力超过了限制的所有系数的设置值。图7 输入力的响应时间4 第三算法下面的控制方程是有效的第三种算法 【3】 :2 zsFDsPIs两边都乘以 s/1得:1zsss(16)自动驾驶仪的结构如图8所示:图8 第三种结构该结构由三环路内,中、外组成。内部循环的形式和以前的例子是相同的,给出了方程(5) 。传递函数包括中间环形式: 22oKsDPw和整个系统的传递函数:322oIsKsKI(17)方程(17)和方程 (11)具有相同的分母 ,所以也具有同样的意义,在 I,P,D 系数中 P 是有效的。图 9显示了时间响应、输入阶跃函数和终值 / 10。图9 角的时间响应图10 输入力的响应时间你可以在图10中观察到的输入力没超过限制,它被表示为红色的限制线。这种结构是最适合 角控制的,因为在以前的例子中输入力超过了限值。Bode 传递函数的特征值由方程(17)给出,如下图所示。图11 波德特性5 非线性分析非线性分析的结构包括倒立摆方程所描述的两种非线性模型模型(1)(2)和推力矢量控制系统的飞机发动机的喷嘴动力学模型通过第二阶传递函数 【4】 给出: 240s其偏转的有限位置为20和60度/秒率 【1】 。该模型提供了关于力的一些计算 【7】 和通过推进系统产生的时刻。在这个例子中唯一的力量音调控制表示为:sinFT (18)其中 T 是喷管的推力,它在模拟过程中其值不变; 矢量喷管偏转和纵向轴之间的夹角。把方程(16)带入方程(18)得: sinzITsDPss(19)让我们假设喷管偏转小角度(约20)是有效的:sin (s )=(S) 。推导出方程(19)的推力 T:1zPIssTs(20)上面提到的方程(20)代表系统的控制律。以下出示了系统的非线性结构:图12 系统的非线性分析新的 P,I,D 值可以通过方程(20)计算和假设喷嘴产生的推力为148 916N,有必要强调,如果飞机的推力是恒定的,那么这些参数就是常数。如果在模拟的过程中推力发生变化,那么这些参数必须根据实际价值去调整推力。注意 P, I, D 值被作为比率。这是非常重要的事实为具有相同的性质的一些类似的系统的实现,如上面提到的。如图12所示的是系统的非线性分析。图13显示了当 Z = 18.8度时的阶跃响应曲线。这是当摆稳定时的最大值。这种限制可以同时计算常数 的值从方程(2)和方程(1)中。从以上得知对于这个摆的运动的限制是不稳定的。图13 角的时间响应如果输入的是以20s 为周期、脉冲宽度为50%的脉冲函数,那么最大的 z值是限制在16.1 的位置。角速度和角速度的响应时间如下图所示。 图14 角的时间响应 图15 角速度的响应时间下图显示的是当 z = 0 和区域随机干扰力50000n 时的倒立摆模型的输入响应曲线。图 16 角的时间响应观察到的最大值 Z 和输入信号频率如图 17、图 18 所示。确定这个值的条件是系统的稳定性。图 17 最大 Z 值 图 18 部分最大的 Z 值对输入力的最大干扰力的频率如图 19 所示。图 19 干扰力从图中知所需的垂直位置的偏差是由输入扰动引起的。这些误差的绝对值,如图 20 所示。图 20 误差绝对值6 结论倒立摆控制中最适合的结构是控制结构(16) ,如图 8 所示。其他结构是不适合的,因为输入力值超过了矢量控制系
- 温馨提示:
1: 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
2: 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
3.本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

人人文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 川公网安备: 51019002004831号
川公网安备: 51019002004831号