目 录
摘 要................................................................Ⅰ
Abstract.............................................................Ⅱ
第1章 绪论..........................................................1
1.1 本课题研究的背景..........................................1
1.2 本课题研究的内容和方法....................................1
1.3国内外的发展现状...........................................1
1.31液压传动发展现状..........................................1
1.3.2 PLC的发展现状...........................................2
第2章 液压传动系统的设计
2.1液压系统工况的分析.........................................2
2.1.1 位移循环图L—t..........................................3.
2.1.2速度循环图v—t...........................................3
2.2液压缸的设计................................................3
2.2.1液压缸的负载分析..........................................3
2.2.2初步确定液压缸的工作压力..................................4
2.2.3液压缸的尺寸计算..........................................5
2.2.4 液压缸流量的计算..........................................5
2.3液压泵的确定与所需功率的计算................................5
2.4阀类元件的选择..............................................6
2.5滤油器的选型................................................8
2.6油箱的设计..................................................8
2.6.1油箱设计要点 .............................................9
2.6.2油箱容量计算..............................................9
第 3 章 滚轮电机的选择和调速 ...........................................9
3.1滚轮电机的选型及计算.........................................9
3.2变频器的选用................................................11
3.3滚轮电机的调速..............................................12
3.3.1三相异步的调速方式........................................12
3.3.2变频器的调速原理..........................................15
第4章 PLC的控制设计..................................................16
4.1 PLC的特点..................................................16
4.2 PLC的选型原则..............................................16
4.3机型的选择.................................................17
4.4控制要求...................................................17
4.5电气原理图..................................................18
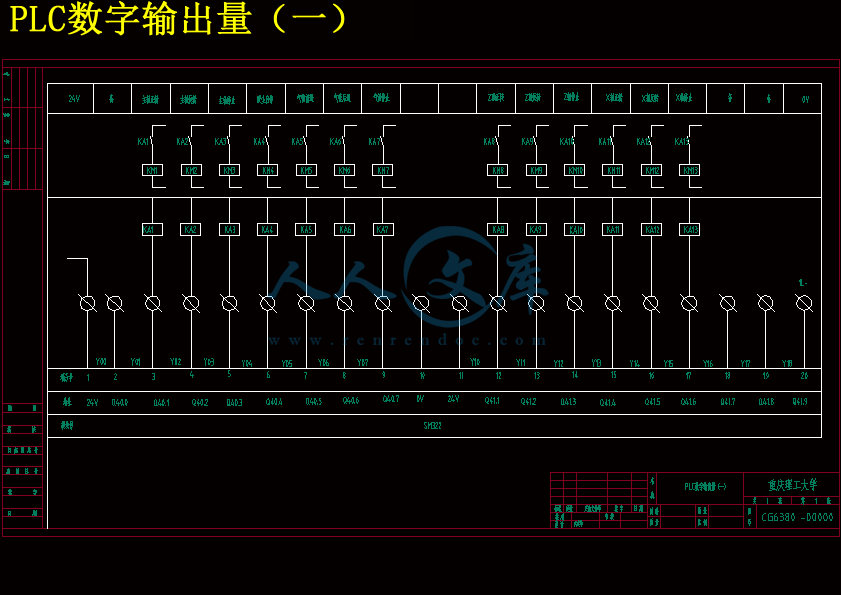
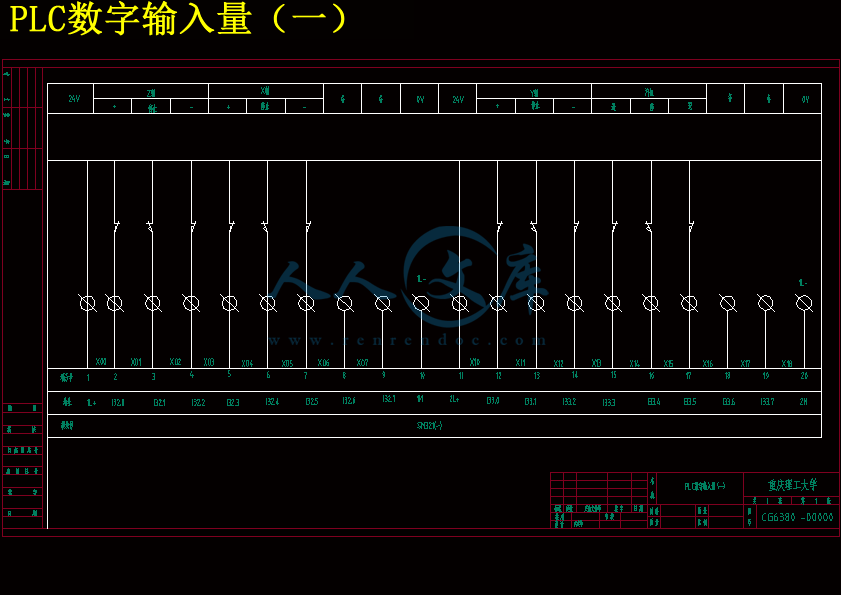
4.6I/O端口分配表..........................................20
4.7电器元件的选型.........................................21
4.8程序设计与系统流程图...................................23
4.9程序设及分析...............................................25
第5章 三菱编程软件和仿真软件.........................................29
5.1三菱编程软件...............................................35
5.2三菱仿真软件...............................................30
结论...................................................................42
致谢...................................................................43
参考文献...............................................................44
第1章 绪论
1.1 本课题研究的背景
心外圆砂带磨床适用于管材、棒材等工件的外圆磨削和抛光,可磨削金属、木材、玻璃、橡胶等材料。随着市场经济的高速发展,对生产的要求也不断提高,对于磨床磨削的要求越来越高,砂带磨床的加工工效甚至超过了普通常规加工工艺,砂带越来越宽,加工精度越来越高,已达到和超过砂轮磨床。如今,由于可编程控制器(PLC)在无心外圆砂带磨床控制系统中的应用范围越来越广泛,为了提高生产效率,PLC控制液压系统对工件上下料在各种机床上也得到了广泛的应用。
1.2 本课题研究的内容和方法
本课题主要是研究PLC控制液压系统,从而在加工生产中实现工件的上下料自动化。而且,这个课题主要是采用实例分析,结合阅读大量的文献和查找资料,寻求出最佳的设计方案。
1.3 国内外的发展现状
1.31 液压传动发展现状
液压传动与控制是以液体(油、高水基液压油、合成液体)作为介质来实现各种机械量的输出(力、位移或速度等)的。它与单纯的机械传动、电气传动和气压传动相比,具有传递功率大,结构小、响应快等特点,因而被广泛的应用于各种机械设备及精密的自动控制系统。液压传动技术是一门新的学科技术,它的发展历史虽然较短,但是发展的速度却非常之快。自从1795年制成了第一台压力机起,液压技术进入了工程领域;1906年开始应用于国防战备武器。
第二次世界大战期间,由于军事工业迫切需要反应快、精度高的自动控制系统,因而出现了液压伺服控制系统。从60年代起,由于原子能、空间技术、大型船舰及电子技术的发展,不断地对液压技术提出新的要求,从民用到国防,由一般的传动到精确度很高的控制系统,这种技术得到更加广泛的发展和应用。
在国防工业中:海、陆、空各种战备武器均采用液压传动与控制。如飞机、坦克、舰艇、雷达、火炮、导弹及火箭等。
在民用工业中:有机床工业、冶金工业、工程机械、农业方面,汽车工业、轻纺工业、船舶工业。
另外,近几年又出现了太阳跟踪系统、海浪模拟装置、飞机驾驶模拟、船舶驾驶模拟器、地震再现、火箭助飞发射装置、宇航环境模拟、高层建筑防震系统及紧急刹车装置等,均采用了液压技术。
总之,一切工程领域,凡是有机械设备的场合,均可采用液压技术。它的发展如此之快,应用如此之广,其原因就是液压技术有着优异的特点,归纳起来液压动力传动方式具有显著的优点:其单位重量的输出功率和单位尺寸输出功率大;液压传动装置体积小、结构紧凑、布局灵活,易实现无级调速,调速范围宽,便于与电气控制相配合实现自动化;易实现过载保护与保压,安全可靠;元件易于实现系列化、标准化、通用化;液压易与微机控制等新技术相结合,构成“机-电-液-光”一体化便于实现数字化



 川公网安备: 51019002004831号
川公网安备: 51019002004831号